
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
» animation ••• , développée de la parabole |
La recherche de l'équation (et de la nature) de la développée de l'hyperbole (enveloppe de ses normales) n'est pas simple.
➔ On peut imaginer sa forme : eu égard à la nature de l'hyperbole (section conique), on peut penser qu'elle ne doit "pas beaucoup" différer, par continuité, de celle de la parabole et de l'ellipse. Mais cette idée est trompeuse car passer d'un plan de section parallèle à une génératrice du cône à un plan parallèle à l'axe du cône peut rejeter des points à l'infini (cas limite), donc dénaturer la courbe attendue.
Partant de l'équation x2 - y2 = 1, pourtant fort sympathique, de l'hyperbole équilatère, l'usage de l'équation générale de la développée conduit à des calculs atroces. De même avec la forme paramétrée de l'hyperbole : x = 1/cos t , y= tan t.
Partant de la forme
élémentaire y = 1/x (en rouge ci-dessous) la même
équation générale conduit à la
paramétrisation 2X = 1/m3 + 3m , 2Y = m3
+ 3/m où m désigne en fait x (abscisse du point courant
de l'hyperbole) : l'équation en (X,Y) des normales
étant ici donnée par Y - 1/x = x2(X - x). La
courbe obtenue (en bleu ci-dessous) rappelle bigrement une "double"
parabole de Neile :

En fait, comme pour l'ellipse, c'est à une courbe de Lamé que nous avons affaire :

La recherche de l'équation se fera sur l'équation réduite de l'hyperbole, dont la représentation pour x > 0 est donnée ci-dessus :
En dérivant par rapport à x, on obtient le coefficient -1/y' des normales à l'hyperbole en un quelconque de ses points M(x,y), à savoir : -a2y/b2x. L'équation en (X,Y) des normales est alors :
ce que l'on peut sans peine mettre sous la forme :
Selon la théorie générale des enveloppes de droites, nous dérivons (e2) par rapport au paramètre qui est ici x en prenant garde à y qui est fonction de x... :
Ce qui nous conduit à :
ou encore :
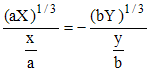
Pour x > 0, l'hyperbole tourne sa concavité vers les x croissants (vers la "droite") et par suite, on a aussi X >0 pour un point de la courbe cherchée. On vérifie facilement l'assertion suivante :
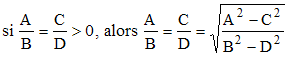
Par conséquent :
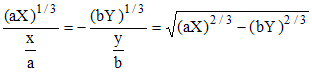
➔ vu (e1), pas de dénominateur au second membre. Quand même, c'est beau les maths... Appelons maintenant et provisoirement R le radical du membre de droite de cette dernière égalité. On a :
Reportons ces valeurs dans l'équation (e2) et mettons R en facteur :
soit, tout simplement :
ou encore plus simple :
En remplaçant R par sa valeur et en divisant par c4/3 :

L'équation de notre développée est bien une courbe de Lamé. Un tout petit couac est lorsqu'on suppose A/B = C/D > 0. Et si ce n'était pas le cas ? on se convaincra que des considérations de parité et de symétrie permettent de penser que l'on ne restreint pas la généralité. Voici les courbes dans leur totalité.
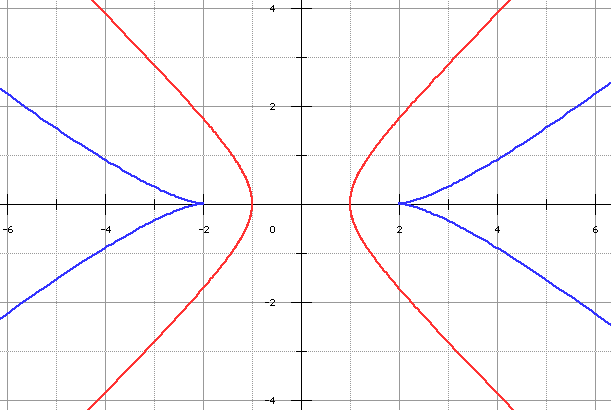
➔ Il est bien clair que l'on peut recommencer avec l'ellipse. Allons-y... non, c'est une blague : plus simple est de passer par l'équation paramétrique x = acos t , y = bsin t :
Cas de l'ellipse : » Autres développées dans ChronoMath : »