ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Étude de la parabole semi-cubique dite parabole de Neile  » parabole cubique      ••• animation

Pionnier dans l'art du calcul de la longueur d'un arc de courbe, le mathématicien anglais Neile chercha à rectifier (rechercher sa longueur) la courbe d'équation cartésienne y² = x³. Cette courbe est en rapport étroit avec la développée de la parabole : enveloppe de ses normales.

On peut utiliser l'équation générale d'une développée mais ce n'est pas très gai. Considérons donc une parabole (p). Par exemple celle d'équation y = x²/4. Le coefficient directeur d'une tangente à (p) en un point M(x_o,y_o) est x_o/2, donc celui de la normale en ce point est -2/x_o. L'équation générale des normales est donc :

Posons m = x_o. On a :

On dérive par rapport au paramètre m :

D'où :

C'est dire que :

Quitte à poser : X = x/2 et Y = (y - 2)/3, on est ramené par affinités à :

et par symétrie par rapport à la première bissectrice des axes (échange de x et de y) :

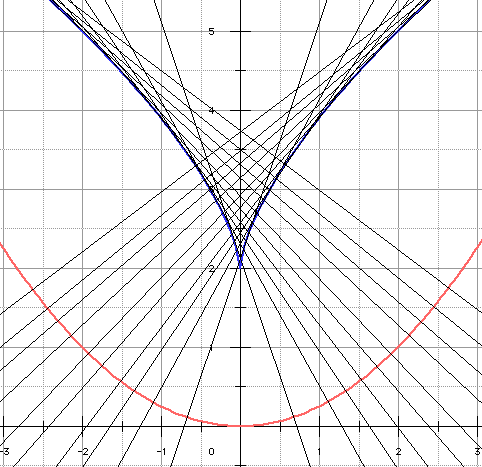
 ➔  La développée, dite parabole semi-cubique, puisque Y = X^3/2 (ou encore : parabole de Neile) est en bleu, la parabole (p) en rose saumon. On a tracé quelques normales à (p) : elles enveloppent la développée... Notons enfin que le calcul d'un arc de cette courbe est plus simple que celui d'un arc de parabole. En effet l'équation y² = x³ fournit par dérivation 2yy' = 3x² et conduit à l'intégrale de la racine carrée de 1 + 9x/4.

Animation :  »