
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
» Une autre preuve géométrique utilisant la puissance d'un point par rapport à un cercle |
|
On montre ici, par une méthode géométrique élémentaire que l'ensemble des points M du plan d'où l'on peut mener deux tangentes perpendiculaires à une ellipse est un cercle, dit cercle de Monge ou cercle orthoptique de l'ellipse.
» Cette étude, écartant toute intrusion analytique, est proposée par François Contensou, professeur d'économie honoraire et passionné de mathématiques ! Nonobstant la notion de cercle directeur et la propriété fondamentale de la tangente à une ellipse, la preuve de l'existence du cercle de Monge ne fait volontairement appel qu'à des notions de géométrie élémentaire : théorème de Pythagore, niveau 3è et théorème d'Apollonius, dit de la médiane, niveau 1ère.
Considérons une ellipse de foyers A et B, ensemble des points M du plan euclidien tels que MA + MB = 2a. On note (Ca) et (Cb) les cercles directeurs associés respectivement à A et B : cercles de centre A et B, de rayon 2a. On pose d'autre part, comme traditionnellement, AB = 2c.
Soit C un point d'où l'on voit l'ellipse sous un angle droit : les tangentes (t) et (t') issues de C, touchant l'ellipse en E et E', sont perpendiculaires.
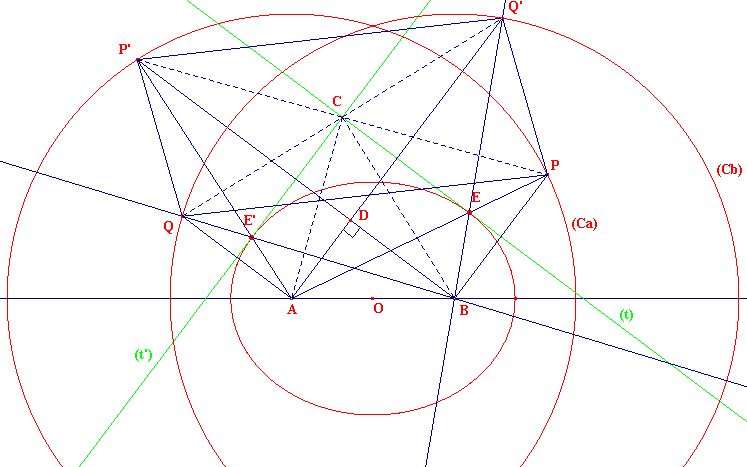
Rappels :
1/
Si (t) est une tangente à l'ellipse, comme (CE) ci-dessus, le symétrique P du foyer B par rapport à cette tangente est situé sur (Ca). » tangente à l'ellipse2/
La composée de deux symétries axiales d'axes perpendiculaires est une symétrie centrale.3/
L'ensemble des points dont la somme des carrés des distances à deux points fixes A et B est constante est un cercle centré au milieu O de [AB]. » preuveL'objectif est de prouver que la somme CA2 + CB2 ne dépend pas de C afin de conclure selon le résultat 3 rappelé ci-dessus.
Selon le rappel 1 :
le symétrique Q du foyer A par rapport à (t) est situé sur (Cb)
le symétrique Q' du foyer A par rapport à la tangente (t') est situé sur (Cb)
le symétrique P' du foyer B par rapport à (t') est situé sur (Ca).
Dans la symétrie d'axe (t), le couple (P,Q) a pour image (B,A) et, dans la symétrie d'axe (t'), le couple (B,A) a pour image (P',Q').
Selon le rappel 2 :
(P,Q) a pour symétrique (P',Q') dans la symétrie centrale de centre C.
Par suite PQ = P'Q' =
BA = 2c et (PQ)//(P'Q') : PQP'Q' est un parallélogramme.

Calculons maintenant P'Q = PQ' : les tangentes (t) et (t') étant perpendiculaires et (BP') étant perpendiculaire à (t'), on a (BP') // (t). De même (AQ') // (t'). (BP') et (AQ') sont donc perpendiculaires en un point D. En appliquant 3 fois le théorème de Pythagore, nous avons :
P'Q2 = P'D2 + QD2 = (AP'2 - AD2) + (BQ2 - BD2) = 8a2 - (AD2 + BD2) = 8a2 - 4c2
Par conséquent, les côtés du parallélogramme PQP'Q' gardent une longueur constante indépendante de C. On en déduit (» exercice corrigé) que la somme des carrés de ses diagonales est constante et égale au double de la somme des carrés des côtés, soit :
QQ'2 + PP'2 = 2(P'Q2 + PQ2) = 2(8a2 - 4c2 + 4c2) = 16a2
D'où, ce qu'il fallait démontrer, car :
CA2 + CB2 = CQ'2 + CP2 = (QQ'2 + PP'2)/4 = 4a2 = cte
L'usage du théorème de la médiane permet de préciser le rayon du cercle décrit par C :
CA2 + CB2 = 2OC2 + AB2/2, donc OC2 = 2a2 - c2 = a2 + b2, car b désignant le demi petit-axe de l'ellipse, on a : a2 = b2 + c2. » ellipse
Conclusion :
L'ensemble des points C est le cercle de centre O, centre de l'ellipse, de rayon r vérifiant r2 = a2 + b2.
➔ Voici la même figure générée au moyen du logiciel de géométrie dynamique Cabri Géomètre, dans sa version CabriJava pour Internet :

Si votre navigateur accepte les applets
Java (»
extension CheerpJ![]() ) :
) :
Vous pouvez déplacer le point M de l'ellipse (a = 3, b = 2, r2
= 5)
Une autre preuve géométrique (puissance d'un point par rapport à un cercle) : »