
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
Usage du tableur » voir aussi #1 , #2 |

Considérons une suite de carrés emboîtés de côté xo, x1, x2, ...xn obtenus en ajoutant à la mesure du côté précédent la mesure de sa diagonale. Les nombres xn sont dits latéraux. Soit yn la diagonale du carré de côté xn. Les yn sont dits, on s'en doute..., diagonaux.
On a xn+1 = xn + yn et selon le théorème de Pythagore :
yn = √2 x xn et yn+1 = √2 × xn+1 = √2 x (xn + yn)
Par conséquent : yn+1 = yn + 2xn
Posons alors rn = yn/xn. Il est aisé de montrer :
![]()
Il est ainsi construit une suite récurrente de la forme rn+1 = f(un) dont il est facile de prouver la convergence vers √2 en choisissant par exemple ro = 1, ce qui correspond à choisir xo = 1 et approximer yo également à cette valeur. Mais nous allons généraliser l'algorithme à la racine carrée d'un nombre positif quelconque :
Soit A un nombre positif; on pose xo = 1, yo = 1, et, pour tout entier naturel n :
xn+1 = xn + yn et yn+1 = yn + Axn
1°/ Prouver que les suites (xn) et (yn) sont strictement croissantes et divergentes.
2°/ Pour n ≥ 2, justifier xn > (1 + A)xn-2; en déduire x2n > (1 + A)n pour tout n ≥ 1.
3°/ Vérifier, par un calcul élémentaire, que :
![]()
En déduire que pour tout n :
![]() » Noter que si A = 2, on retrouve une
équation de Pell.
» Noter que si A = 2, on retrouve une
équation de Pell.
4°/ On pose, pour tout entier naturel n : rn = yn/xn et vn = r2n. Montrer que l'on a :
![]()
5°/ Poser rn+1 = f(rn); exprimer f et vérifier que :
si 0 < A < 1, alors f est strictement croissante et la suite (vn) converge en décroissant vers √A, l'erreur à chaque itération n'excédant pas :

si A > 1, alors f est strictement décroissante et la suite (vn) converge en croissant vers √A, l'erreur à chaque itération n'excédant pas :

6°/ On pose wn = r2n+1. Montrer que les suites (vn) et (wn) sont adjacentes : c'est à dire :
l'une est croissante majorée par √A tandis que l'autre est décroissante minorée par √A;
lim (vn - wn) = 0.
➔ On obtient ainsi un encadrement de la racine carrée cherchée et un calcul très simple de l'erreur commise.
| 7° a/ Programme 1 : |
Calcul des vn = r2n :
Le calcul de r2n se programme très facilement sur tableur (ici Microsoft Excel). Partant de xo et yo (ligne 2) on obtient x2n en calculant xn+2 = (A + 1)xn + 2yn. De même y2n = (A + 1)yn + 2Axn.
On écrit ces formules en ligne 3; on exprime r2n = y2n/x2n; A est placé en H1, cellule que l'on nomme A, et l'erreur est calculée suivant que A est < 1 ou > 1. On recopie vers le bas autant de fois que voulu.
♦ Formulation :

♦ Exécution :

! L'inconvénient de la méthode est, que pour A > 1, (A ± 1)n devient "rapidement" très grand et pose des problèmes de dépassement de capacité. On peut contourner provisoirement la difficulté en recourant aux logarithmes :
Programme JavaScript : »
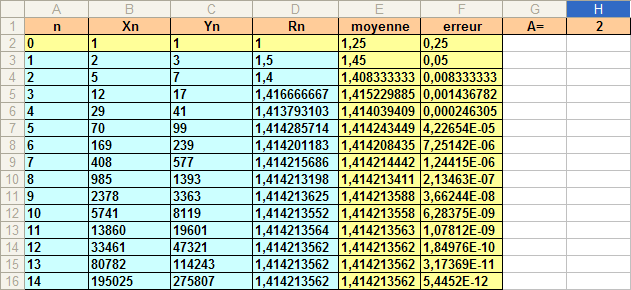
| 7° b/ Programme 2 : |
Calcul simultané des des r2n et r2n+1 :
On prend comme valeur approchée de √A le nombre (r2n + r2n+1)/2. L'erreur à chaque itération est alors inférieure à | r2n - r2n+1 |/2, soit, sur tableur : ABS(D2 - D3)/2. Les formules sont écrites en ligne 3. On recopie vers le bas autant de fois que voulu.
♦ Formulation :

♦ Exécution :
➔
Si vous
utilisez Microsoft Excel, vous pouvez télécharger les fichiers :
theon_algo.zip