ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Théorème du papillon           niveau prof...

Voici un exercice relativement difficile de géométrie euclidienne élémentaire d'apparence banale. Il intéressa bon nombre de mathématiciens, dont William Horner et Eric T. Bell. Le mathématicien français Jean-Pierre Kahane y fit allusion récemment (visionnez la vidéo indiquée sur la page qui lui est consacrée).

L'approche projective proposée par David Ruelle dans son livre L'étrange beauté des mathématiques (Ed. Poche Sciences, 2008) est certes esthétique mais dire que ce petit problème relève de la géométrie projective plutôt que de la géométrie euclidienne est excessif : La résolution ici présente, empruntée à Harold Coxeter dans son livre Redécouvrons la géométrie, (Éd. Dunod, 1971) fait intervenir la notion euclidienne élémentaire, mais aujourd'hui délaissée, des triangles semblables (conséquence de la propriété de Thalès) et, sans obligation, une pincée de puissance d'un point par rapport à un cercle...

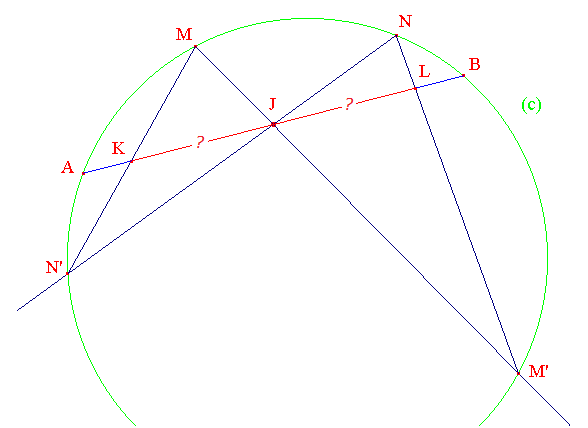
• Soient (c) un cercle et une corde [AB] de ce cercle. On note J son milieu;

• Soient deux autres cordes [MM'] et [NN'] passant par J;

• [MN'] coupe [AB] en K, [NM'] coupe [AB] en L.

Montrer que J est aussi le milieu de [KL]

Considérer les projections orthogonales de K et L comme indiquées ci-dessous. Poser, pour simplifier, JK = x, JL = y et JA = JB = a. Faites apparaître des rapports égaux en constatant la présence de 6 couples de triangles semblables. On évaluera d'abord x²/y²...

J sera le milieu de KL si JK/JL = 1. La présence de quelques angles inscrits de même mesure nous incite à faire apparaître des triangles semblables permettant de faire apparaître des rapports égaux. Pour ce faire projetons d'une part K en E et F respectivement sur [MJ] et [JN'], d'autre part L en G et H respectivement sur [NJ] et [JM']. Posons x = JK et y = JL.

Les triangles KN'F et LM'H sont semblables :

• Les triangles EJK et HJL sont semblables : JK/JL = x/y = KE/LH.

• Les triangles FJK et GJL sont semblables : x/y = KF/LG.

• Les triangles MEK et NGL sont semblables : KE/LG = MK/NL.

• Les triangles N'FK et M'HL sont semblables : KF/LH = N'K/M'L.

• Les triangles N'FK et M'HL sont semblables : KF/LH = N'K/M'L.

Les deux premières proportions montrent que :

Les deux dernières montrent que :

Les cordes [MN'] et [AB] se coupant en K déterminent les triangles semblables ALN' et MBK :  en termes de puissance de K par rapport au cercle (c), on peut écrire : KM × KN' = KA × KB. De même, LN × LM' = LA × LB. Donc, en posant JA = JB = a :

Ce qui implique a²x² = a²y², d'où x = y : ce qu'il fallait démontrer.