ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Dérivées partielles & extremum #3     niveau sup     » Voir : #1 , #2 | Volume maximal  | extremums de f(x,y) = x3 + y4 - yx2 - xy2  méthode de Hesse

Étant donné un triangle ABC et un point M du plan, la géométrie élémentaire nous apprend que le centre de gravité G du triangle est l'unique point du plan maximisant le produit des distances de M aux côtés du triangles.

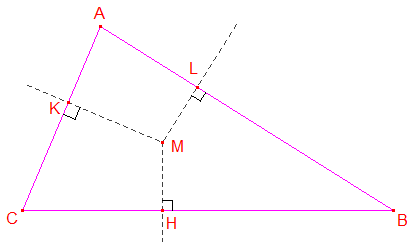
Autrement dit : le produit MH x MK x ML est maximal si et seulement si M = G

Si on se place dans un repère euclidien en posant A(a,a'), B(b,b'), C(c,c') et M(x,y), on peut écrire le produit MH x MK x ML en tant fonction de R² dans R et retrouver que G est la solution minimale en étudiant les points critiques de f. Mais comme l'écrit David Delaunay (professeur MP/MPSI, lien ci-dessous), le calcul est lourd même en se ramenant à A(1,0) et B(0,1) sans pour autant restreindre la généralité.

Mais avant de découvrir la solution proposée par David Delaunay, remarquer que l'on peut rechercher M en tant que barycentre du système pondéré {(A,a), B,b), C,c)} avec a + b + c = 1. Les poids a, b et c son non nuls, sinon M serait sur le pourtour du triangle, ce qui annulerait le produit et un tel M ne peut être solution !

Montrer que la fonction f(a,b) = ab(1 - a - b) avec a > 0, b > 0, a + b < 1 admet un unique extremum et que ce dernier est un maximum.

Rappel :   

Soit f une fonction de deux variables u et v de classe C² (deux fois continument dérivable) au voisinage d'un point (u_o,v_o) et admettant en ce point un extremum (annulant donc ses dérivées partielles premières). Posons, en omettant les variables (u_o,v_o) afin de simplifier les écritures:

• Si Δ > 0 : f admettra un minimum (resp. un maximum), suivant que ∂²f/∂u² (ou ∂²f/∂v² qui possède alors le même signe) est strictement positive (resp. négative).

• Si Δ < 0 : ni maximum, ni minimum.

• Si Δ = 0 : cas douteux.

Si vous séchez après avoir bien cherché : ››››

f(a,b) = ab(1 - a - b) avec a > 0, b > 0, a + b < 1

1°/ On recherche les points critiques de f, c'est à dire les couples (a, b) annulant ∂f/∂a et ∂f/∂b :

• ∂f/∂a = b - 2ab - b² = b(1 - 2a - b),  ∂f/∂b = a - 2ab - a² = a(1 - 2b - a)

• a et b n'étant pas nuls, on est en présence du système 2a + b = 1, a + 2b = 1 conduisant à a = b = 1/3 > 0 et a + b = 2/3 < 1.
  Ce qui fournit un unique point critique acceptable.

Il s'agit maintenant de montrer qu'il s'agit bien d'un maximum sous les conditions :

• ∂²f/∂a² = -2b = -2/3 < 0 ,  ∂²f/∂b² = -2a = -2/3 < 0  ,  ∂²f/∂a∂b = 1 - 2a - 2b = -1/3.
  Donc Δ = ∂²f/∂a² x ∂²f/∂b² - (∂f/∂a∂b)² = 1/3 > 0.
      En vertu du résultat rappelé, le couple (1/3,1/3) est l'unique point maximisant f.

Tout cela fait penser au centre de gravité du triangle ABC...

Rappel :  

• Dans le plan rapporté à un repère orthonormé, l'aire d'un triangle ABC n'est autre que ½ |det(AB, AC)| : » Gibbs.

• distance d'un point à une droite :  » droites du plan.