ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 

Équation différentielle du 1er ordre et courbes intégrales #3             Extrait BTS indus 1986   » #1 , #2       » voir aussi...

On considère l'équation différentielle du 1er ordre :

(e) :        xy² + x²(x + 1)yy' = 5 - 3x , x∈]0,+∞[             

1°) En posant z = y², montrer que (e) se ramène à l'équation différentielle linéaire d'inconnue z :

(e') :        xz + x²(x + 1)z' = 10 - 6x

2°) Donner la solution générale de l'équation (e').

3°) Donner une équation de la courbe intégrale passant par A(1,0).

1°) et 2°) On a z' = 2yy' et par  remplacement, on trouve sans difficulté xz + x²(x + 1)z' = 10 - 6x. On résout tout d'abord l'équation homogène xz + x²(x + 1)z' = 0 qui se ramène à :

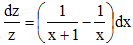
fournissant

Afin de trouver une solution particulière de l'équation complète, on utilise la méthode de la variation de la constante, on obtient :

On décompose le second membre en éléments simples (procéder par identification) :

D'où k = 16/(x + 1) + 10ln |x/(x + 1)| et une solution particulière est alors :

Eu égard à l'ensemble de définition de l'équation, on peut omettre la valeur absolue dans la partie logarithmique. La solution générale de l'équation donnée est alors :

et une équation de la solution dont la courbe intégrale passe par A(1,0) correspond à k = 10ln2 - 8.