ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Bicorne (en forme de chapeau bicorne de l'époque napoléonienne)         »  Voir l'animation

Cette courbe algébrique fermée du 4ème degré (quartique) est une des nombreuses courbes étudiées par G. de Lonchamps dans  son Journal de Mathématiques spéciales (Note sur le bicorne, 1897) :

• Dans un repère orthonormé d'origine O, on considère deux cercles (a) et (b) de centres A(0,-a) et B(0,a).

• Un point P décrit le cercle (b); soit (p) la polaire de P par rapport au cercle (a).

• La perpendiculaire à (Ox) passant par P coupe (p) en M. L'ensemble des points M est le bicorne.

Si l'on pose P(x,Y) et M(x,y), en écrivant d'une part que P décrit le cercle de centre B, de rayon a, d'autre part que la division [P,M,m₁,m₂] est harmonique, on obtient :

x² + (Y - a)² = a²  et  a/Y = (Y - 2a - y)/(Y + y)

et, par là, le système :

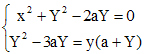
 ➔  La division harmonique [P,M,m1,m2] permet d'écrire (en valeurs algébriques) Pm₁/Pm₂ = - Mm₁/Mm₂. Remarquer que cette relation ne fait intervenir que des ordonnées, que P et m₂ ont des ordonnées opposées et que si m est le symétrique de m par rapport à Ox, on a la relation  y_m + Y = 2a

On élimine maintenant Y² au profit de Y, on reporte dans la 1ère équation. On obtient l'équation cartésienne du bicorne : (a² - x²)(a + y)² = (x² + a² + 2ay)². Par changement d'origine, translation de vecteur u(0,+a), le bicorne se retrouve posé sur l'axe des abscisses et son équation devient plus sympathique... :

(a² - x² - 2ay)² = y²(a² - x²)

L'équation peut également s'écrire sous la forme y = f(x) au moyen d'une double détermination :

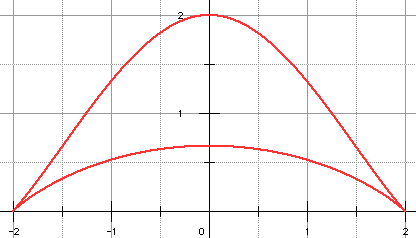
Ci-dessus, la courbe est obtenue pour a = 2. Les points de coordonnées (±2; 0) sont des points de rebroussement de première espèce.

 Les tangentes en ces points sont perpendiculaires en le sommet de la courbe. La branche inférieure (resp. supérieure) est obtenue par le signe + (resp. signe -) devant le radical.

 ➔  Le bicorne est aussi une courbe unicursale, c'est à dire représentable paramétriquement : en posant x = a.cos t, on obtiendra (relativement...) facilement :

y = a.sin²t /(2 + sin t) ou y = a.sin²t /(2 - sin t)

Si votre navigateur accepte les applets Java (» extension CheerpJ) :
Déplacer P; pour effacer le lieu double-cliquer dans la figure