
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
» construction de la section dorée selon Euclide niveau 3ème/Ter |
1. Dans son livre XIII, Euclide énonce et démontre la proposition suivante :
PROPOSITION III
Si une ligne droite est coupée en extrême et moyenne raison, le quarré du plus petit segment augmenté de la moitié du plus grand segment est égal au quintuple du quarré de la moitié du plus grand segment
Votre mission : traduire en langage
actuel et vérifier l'assertion...
! distinguer (a + b/2)2
: carré de a augmenté de la moitié de b
et a2 + b/2 : carré de a,
augmenté de la moitié de b
!
2. Dans son livre XIII, Euclide énonce et démontre la proposition suivante :
PROPOSITION VIII
Si des droites soutendent deux angles de
suite d'un pentagone équilatéral et équiangle,
ces droites se couperont en
extrême et moyenne raison, et leurs plus grands segments
seront égaux au côté du
pentagone.
∗∗∗ Pourriez-vous démontrer cela ? Liens utiles ici, ci-dessous ou par ici...
Voici la preuve apportée par Euclide :
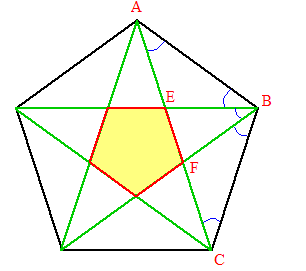
Deux angles inscrits, interceptant des arcs de même mesure, ont même mesure : AEB est donc isocèle;
On montre ensuite très facilement que les triangles AFB et BEC sont isocèles;
Les triangles ABC et ABE sont semblables;
il s'ensuit que : AB/BE = BC/EA = AC/BA;
Mais AB = AF = CB et EA = EB.
Vous en déduisez que : AF/AE = AC/AF.
CQFD