
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
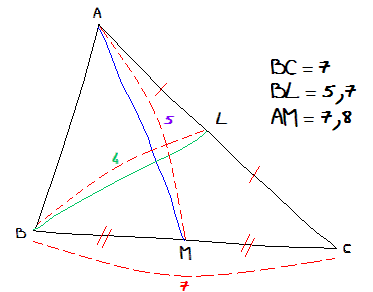
» #1 à 4 , #5 , #7 , #8 , #9 , #10 » Variante : en ne connaissant que les 3 médianes |
 On
rappelle ou on admettra que
: dans un triangle, les médianes sont les
droites passant par un sommet et le milieu du côtés opposé. En fait, on les
assimile souvent à un segment (comme [AA'] ci-dessus à droite).
On
rappelle ou on admettra que
: dans un triangle, les médianes sont les
droites passant par un sommet et le milieu du côtés opposé. En fait, on les
assimile souvent à un segment (comme [AA'] ci-dessus à droite).
Elles sont concourantes en un point G (centre de gravité du triangle) situé au tiers de chaque médiane à partir de leur « pied » qui sont les milieux des côtés du triangle : on a donc par exemple AG = 2GA'.

Si tu sèches après avoir bien cherché : ››››
| Solution : |
Analyse :
Le codage indique que [BL] et [AM] sont deux médianes du triangle ABC. Elles se coupent en G (centre de gravité du triangle) au 2/3 de chaque sommet et au 1/3 à partir de leur base.
5,7 ÷ 3 = 1,9 et 7,8 ÷ 3 = 2,6. Ainsi :
BG = 3,8 et MG = 2,6
Or BM = 7 ÷ 2 = 3,5. D'où la construction :
Construction :
On construit le triangle BMG (règle graduée et compas);
Placer C, symétrique de B par rapport à M;
Placer A sur [MG) de sorte que MA = 7,8;
Tracer [BA] et [BC].

Synthèse :
On est assuré d'avoir BL = 5,7. En d'autres termes, si on place L avant de tracer [AC], on est assuré que L est le milieu de [AC] car la construction de G au tiers de la médiane AM oblige (BG) à couper [AC] en son milieu et [BL] à mesurer 3 x 1,9 = 5,7.
 Toute construction doit être conduite par analyse
et synthèse. L'analyse est le raisonnement aboutissant à la
construction cherchée. Mais le processus d'analyse procède par implication : si
ABC existe (on suppose la construction aboutie) alors on a nécessairement (forcément
en langage élève) ceci ou cela, donc on va faire ceci ou cela.
Toute construction doit être conduite par analyse
et synthèse. L'analyse est le raisonnement aboutissant à la
construction cherchée. Mais le processus d'analyse procède par implication : si
ABC existe (on suppose la construction aboutie) alors on a nécessairement (forcément
en langage élève) ceci ou cela, donc on va faire ceci ou cela.
La synthèse consiste à vérifier que ces conditions nécessaires aboutissant à la construction sont aussi suffisantes, c'est à dire que cette construction vérifie bien toutes les hypothèses de l'énoncé.