ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 
Projection
orthogonale plane d'une hélice circulaire
» hélice, spirale hyperbolique , cochléoïde |
Dans un repère orthonormé (0,x,y,z), on considère une hélice circulaire d'axe (Oz) tracée sur un cylindre de rayon R. On sait que son équation, sous forme paramétrée, est de la forme :
➔ La simplicité de l'équation dépend d'un bon choix du repère choisi dans (P) pour "voir" la courbe projetée : bon choix du point de vue de l'observateur : c'est un problème de perspective. Un choix quelconque engendrerait une courbe vue "de travers" et, par là, une équation complexe nécessitant un changement de repère, difficile à déterminer, afin de reconnaître la nature de la courbe obtenue.
Vu que l'hélice est d'axe (Oz), nous choisissons un repère orthonormé (O,X,Y) du plan (P) de projection de sorte que (Ox) soit le projeté orthogonal de (Oz) : la courbe sera ainsi vue comme possédant un axe de symétrie parallèle à (OY) :
Étudions tout d'abord le projeté orthogonal M(x',y',z') d'un point m(x,y,z) de l'espace sur le plan (P) : x + y + z = 0. Il suffit d'écrire que (mM) est orthogonale à (P) et que M est un point de (P).
♦ D'une part, vectoriellement :
donc : x' - x = y' - y = z' - z = λ où λ est une constante à déterminer
♦ D'autre part :
♦ Par suite : λ = -(x + y + z)/3 et nous aurons :
3x' = 2x - y - z
3y' = -x + 2y - z
3z' = -x - y + 2z
Le vecteur directeur de (Oz) a pour coordonnées (0,0,1). On peut alors choisir I(1,1,-2)/√6 comme premier vecteur de base normé de (P) puis J(1,-1,0)/√2 pour constituer un repère orthonormé (O,I,J) de (P).
Soit M(X,Y) un point de la courbe cherchée, on identifie en écrivant les deux écritures de OM dans (P) :
On obtient sans difficultés :
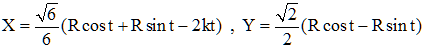
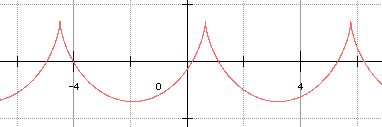
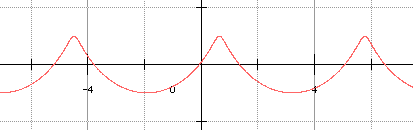
cos t + sin t = √2.cos(t - π/4) et cos t - sin t = - √2.sin(t - π/4). En posant θ = t - π/4, la courbe obtenue, a une équation de la forme :
Quitte à changer θ en π/2 - θ pour changer sin en cos et vice versa, on reconnaît l'équation d'une cycloïde éventuellement allongée ou raccourcie, ayant subi une affinité de rapport c/a d'axe (OY) suivant que a = b , a > b ou a < b. Dans notre cas : a = R√3/3 , b = k√6/3.
