ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Équation selon l'Encyclopédie de Diderot et d'Alembert

 ➔   Texte original. Seuls sont modifiés la mise en page, quelques tournures et aspects orthographiques ou grammaticaux Les mots ou les commentaires en vert sont ajoutés pour une meilleure compréhension.

ÉQUATION, s. f. (substantif féminin) en Algèbre, signifie une expression de la même quantité présentée sous deux dénominations différentes.

Ainsi quand on dit 2 x 3 = 4 + 2; cela veut dire qu'il y a équation entre deux fois trois et quatre plus deux.

On peut définir l'équation (comme) un rapport d'égalité entre deux quantités de différentes dénominations, comme quand on dit 60 sous = 3 livres ou 20 sous = 1 livre. ou b = d + e, ou 12 = (a + b) /5, etc.

Ainsi mettre des quantités en équation, c'est représenter par une double expression des quantités réellement égales et identiques.

    

i/  Le sou et la livre étaient des unités monétaires employées autrefois. Le sou fut une pièce frappée en or, en argent puis en cuivre (dès le règne de Louis XIV). La livre apparaît avec les Valois (dès 1328). Elle correspond alors, en poids, à la valeur d'une livre d'argent (d'où le terme argent -et de sou- pour parler de la monnaie). Une livre valait 20 sous. Après la Révolution, le franc a remplacé la livre et le sou fut remplacé par la pièce de 5 centimes valant un vingtième du franc : 100 centimes = 1 franc. Depuis Janvier 2000, le franc a disparu au profit de l'euro. Adieu jolie semeuse...

ii/ On voit ici que l'on ne fait pas de distinction claire entre équation et égalité. Une définition que l'on pourrait donner, aujourd'hui d'une équation serait une égalité où apparaissent des nombres et des lettres représentant des nombres, appelées inconnues, et qu'il s'agit de calculer afin que l'égalité soit numériquement vérifiée : 2 x 3 = 4 + 2 n'est pas, de nos jours, une équation. 60 sous = 3 livres non plus. Ni b = d + e si l'on ne spécifie pas les lettres connues (paramètres) et les lettres inconnues. 12 = (a + b)/5 est une équation à deux inconnues dont a = 40 et b = 20 est une solution (il y a là une infinité de solutions).

Le caractère ou le signe d'équation est = ou ; ce dernier est plus fréquent dans les anciens algébristes (Descartes utilisa ce signe, Pacioli utilisa simplement _ ), et l'autre dans les modernes (dû à Recorde).

La résolution des problèmes par le moyen de leurs équations, est l'objet de l'Algèbre.

Membres d'une équation, ce sont les deux quantités qui sont séparées par le signe = ou; et termes d'une équation, ce sont les différentes quantités ou parties, dont chaque membre de l'équation est composé, et qui sont jointes entre elles par les signes + et -. Ainsi dans l'équation :

b + c = d

et l'équation signifie que la seule quantité d est égale aux deux b et c prises ensemble.

 Recorde et le signe d'égalité : »

Les équations, eu égard à la puissance plus ou moins grande à laquelle l'inconnue y monte, se divisent en équations simples, quarrées, cubiques, etc. :

On peut considérer les équations sous deux points de vue, ou comme les dernières conclusions auxquelles on arrive dans la solution des problèmes, ou comme les moyens par lesquels on parvient à la solution finale.

Les équations de la première espèce ne renferment qu'une quantité inconnue mêlée avec d'autres quantités données ou connues; celles de la seconde espèce renferment différentes quantités inconnues qui doivent être comparées et combinées ensemble, jusqu'à ce que l'on arrive à une nouvelle équation qui ne renferme plus qu'une inconnue mêlée avec des connues.

Pour trouver la valeur de cette inconnue, on prépare et on transforme l'équation de différentes manières qui servent à l'abaisser à un moindre degré et à la rendre la plus simple qu'il est possible.

La théorie et la pratique des équations, c'est-à-dire la solution des questions par les équations, a plusieurs branches ou parties.

  1. La dénomination qu'on doit donner aux différentes quantités en les exprimant par les signes ou symboles convenables.

  2. La réduction du problème en équation (mise en équation).

  3. La réduction de l'équation même au degré le plus bas et à la forme la plus simple.

  4. On y peut ajouter la solution de l'équation ou la représentation de ses racines par des nombres ou des lignes (solution géométrique).

Nous allons donner d'abord les règles particulières aux deux premiers articles, c'est-à-dire en général la méthode de mettre en équation une question proposée.

Une question ou un problème étant proposé, on suppose que les choses cherchées ou demandées sont déjà trouvées, et on les marque ordinairement par les dernières lettres x, y, z, etc. de l'alphabet, marquant en même temps les quantités connues par les premières lettres de l'alphabet, comme b, c, d, etc. (les paramètres).

Toutes les quantités qui doivent entrer dans la question, étant ainsi nommées, on examine si la question est sujette à restriction, ou non, c'est-à-dire si elle est déterminée ou indéterminée. Voici les règles par lesquelles on peut le savoir.

  1. S'il y a plus de quantités inconnues qu'il n'y a d'équations données ou renfermées dans la question, le problème est indéterminé, et peut avoir une infinité de solutions. Quand les équations ne sont pas expressément contenues dans le problème, on les trouve par le moyen des théorèmes sur l'égalité des grandeurs.

  2. Si les équations données ou renfermées dans le problème sont précisément en même nombre que les quantités inconnues, le problème est déterminé, c'est-à-dire n'admet qu'un nombre de solutions limité.

  3. S'il y a moins d'inconnues que d'équations, le problème est plus que déterminé, et on découvre quelquefois qu'il est impossible par les contradictions qui se trouvent dans les équations (...).

Exemple : un marchand augmente tous les ans son bien d'un tiers, en ôtant 100 livres qu'il dépense par an dans sa famille, au bout de trois ans il trouve son bien doublé. On demande combien ce marchand avait de bien au commencement de ces trois ans.

Pour résoudre cette question, il faut bien prendre garde aux différentes propositions qu'elle renferme, et qui fourniront les équations (expressions) suivantes :

 
(Texte original, BNF)
Soit x le montant du bien demandé :

La question se réduit donc à résoudre cette équation :

(64x - 14800)/27 = 2x

par le moyen de laquelle on trouvera la valeur de x de la manière suivante :

Ainsi ce marchand avait 1480 livres de bien.

 Version "modernisée" (exercice niveau 2nde) :  »

Il résulte de ce que nous venons de dire, que pour résoudre les questions qu'on propose sur les nombres ou sur les quantités abstraites, il ne faut presque que les traduire du langage ordinaire en langage algébrique, c'est-à-dire en caractères propres à exprimer nos idées sur les rapports des quantités.

Il est vrai qu'il peut arriver quelquefois, que le discours dans lequel l'équation est proposée ne puisse être rendu algébriquement; mais en y faisant quelques petits changements et ayant principalement égard au sens, plutôt qu'aux mots, la traduction deviendra assez facile. La difficulté qui peut se rencontrer dans cette traduction vient uniquement de la différence des idiomes, comme dans les traductions ordinaires. Cependant pour faciliter la solution de ces sortes de problèmes, nous allons en donner un exemple ou deux.

1°. Étant donné la somme de deux nombres a, et la différence de leurs carrés b, trouver les (ces) nombres; supposons que le plus petit de ces nombres soit x, l'autre sera a - x, et les quarrés seront xx, et aa - 2ax + xx, dont la différence est aa - 2ax, qui doit être égale à b; donc aa - 2ax = b; donc aa - b = 2ax et

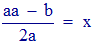
       (Texte original, BNF)

2°. Trouver trois quantités x, y, z dont on suppose connues les sommes de deux quelconques d'entre elles.

Supposons que la somme de x et de y soit a, que celle de x et de z soit b, et que celle de y et de z soit c, on aura les trois équations x + y = a, x + z = b, y + z = c; pour chasser maintenant deux des trois quantités x, y, z, par exemple, z et y, on aura par la première et par la seconde équation y = a - x et z = b - x; on substituera dans la troisième équation ces valeurs au lieu de y et de z, et l'on aura a - x + b - x = c, et

x étant trouvée, on aura y et z par le moyen des équations y = a - x et z = b - x.

Par exemple, si la somme de x et de y est 9, celle de x et de z, 10, et celle de y et de z, 13; dans les valeurs de x, y et z, on écrira 9 pour a, 10 pour b, et 13 pour c, et on aura a + b - c = 6, par conséquent

y ou a - x = 6 et z ou b - x = 7.   

→ les ou ci-dessus, comme dans y ou a - x, expriment c'est à dire.

(...)  4°. Une personne voulant distribuer trois sous à un certain nombre de pauvres, trouve qu'il lui manque huit sous; ainsi elle ne leur donne à chacun que deux sous, et elle a trois sous de reste. On demande combien cette personne avait d'argent, et combien il y avait de pauvres ?

Soit x le nombre des pauvres; et comme il s'en faut huit sous qu'ils ne puissent avoir trois sous chacun, l'argent est donc 3x - 8, dont il faut ôter 2x, et il doit rester 3; donc 3x - 8 - 2x = 3 ou x = 11.

(...) Jusqu'ici nous n'avons fait que traduire l'article équation à peu près tel qu'il se trouve dans l'Encyclopédie anglaise. Cet article est tiré presque en entier de l'Arithmétique universelle de M. Newton; il est aisé d'y reconnaître en effet la main d'un grand maître, et nous avons cru devoir le donner tel qu'il est par cette raison, l'Arithmétique universelle n'ayant point d'ailleurs été traduite jusqu'ici en notre langue. Mais il reste encore sur la théorie des équations beaucoup de choses à dire pour rendre cet article complet dans un ouvrage tel que l'Encyclopédie.

(...)

Jean le Rond d'Alembert

© Serge Mehl - www.chronomath.com