ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Calcul du côté de l'ennéagone régulier selon Al-Biruni                    » Polygones réguliers

  » Ennéagone :  du grec ennéa = neuf  et gônia  = angle  : polygone qui a 9 angles, donc 9 côtés

Vu que 360 ÷ 9 = 40, construire l'ennéagone régulier revient à trisecter l'angle de 120°. Mais on sait depuis Wantzel que la trisection d'un angle, au sens d'Hippias (à la règle et au compas), est généralement impossible : 120° n'est pas trisectable, car  sa  moitié ne l'est pas.

Pierre-Laurent Wantzel, trisection & exceptions : »

Conscient du problème, datant alors de 1500 ans déjà, Al-biruni s'attaque au polygone régulier de 18 côtés, dont l'angle au centre mesure alors 20°, avec l'intention de calculer le côté de l'ennéagone en fonction du rayon qu'il prend égal à l'unité. La figure obtenue s'analyse alors très simplement :

On considère un cercle de centre O de rayon et deux points A et B de ce cercle tels que ^AOB = 20°.

• Soit C le point de [OB] tel que AB = AC. Il est clair que l'on a AC < AO; on admettra ce résultat.

• Soit D le point de [AO] tel que AC = AD

 

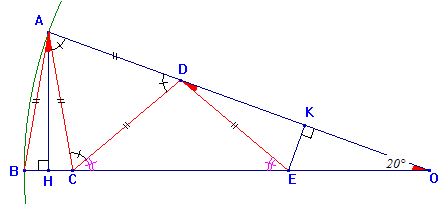
1°/ Montrer que ^BAC = 20°.

2°/ En remarquant que les triangles ABC et AOB sont semblables (on peut se ramener à une configuration de Thalès), montrer que BC/AB = AB/OA; en déduire que si l'on prend OA comme unité, on a BC = AB².

3°/ Montrer que le triangle ACD est équilatéral.

• On note E le point de [BC], autre que C tel que DC = DE, H le projeté orthogonal de A sur [BC] et K le projeté orthogonal de E sur [OA]. On pose désormais OA = 1 et x = AB.

4°/ Montrer que OED est isocèle et que OE = x.

5°/ En remarquant que les triangles AHO et EKO sont semblables (on peut se ramener à une configuration de Thalès), montrer que OH/OK = 1/x.

5°/ Montrer que OH = 1 - x²/2 et OK = (1 - x)/2; en déduire :

x³ = 3x - 1

A la manière des mathématiciens grecs qui, faute de construction à la règle et au compas, durent tolérer les calculs fractionnaires approchés (par approximations successives), il s'agit alors de calculer deux moyennes proportionnelles x et y telles que :

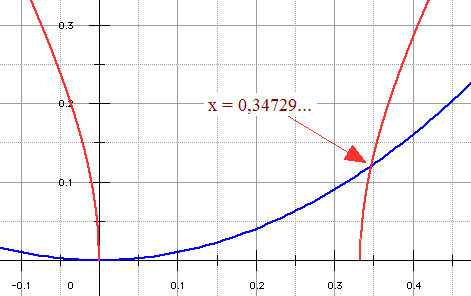
Ce qui revient à intersecter la parabole d'équation y = x²  avec l'hyperbole y² = 3x² - x :

Par des moyens algébriques plus sophistiqués, on peut appliquer la formule de Cardan :

Résolution de l'équation (entrez a = 1, b = 0, c = -3, d = 1) :  »

Votre ordinateur a dû vous répondre quelque chose comme ci-dessous :

Sachant que 0 < x < 1, nous choisissons x = 0,347296... et d'après la théorie des demi-cordes, cela doit être 2 × sin 10°, ce qui est bien le cas.

Le côté de l'ennéagone est y = 2AH. Or AH² = x² - (x²/2)² ,  donc :

et on peut vérifier que cela n'est autre que y = 2 x sin20° , soit : y = 0,684040... correspondant à la formule :

AB = 2R × sin ^AOB