ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 
Développante de
chaînette
»
étude de la chaînette |
Nous appliquons ici les résultats exposés à la page développante d'une courbe afin de les appliquer à la recherche à la développante de la chaînette par rapport à son sommet A.
L'équation cartésienne de la chaînette est : y = a.cosh(x/a). Nous choisissons le cas simplifié a = 1 (cosinus hyperbolique). On a alors A(0,1). La longueur d'arc s sur, l'intervalle [0,x], est facile à calculer : s = sinh x. Dans ces conditions, paramétrons la courbe y = cosh x en posant :x = α et y = cosh α
On a x' = dx/dα = 1 , y' = dy/dα = sinh α , n2 = x'2 + y'2, d'où n = cosh α (» développante). Nous avons alors pour équation de la développante par rapport à A(0,1) :
X = α - sinh α/cosh α , Y = cosh α - sinh2 α/cosh α, soit : X = α - tanh α , Y = 1/cosh α
C'est l'équation d'une tractrice. On vérifie en effet facilement qu'avec les notations ci-dessus et û = ^(Ox,MT), on a :
Y'/X' = tan û = -1/sinh α, puis sin û = 1/cosh α , cos û = - tanh α.
Mais tan û = 2tan(û/2)/(1 - tan2(û/2)) : Posons t = tan(û/2). Il vient : -2/(eα - e-α) = 2t/(1 - t2), soit : eα/(e2α - 1) = t/(t2 - 1). C'est dire que eα = tan(û/2) et l'équation de la développante peut alors s'écrire :
X = ln | tan(û/2) | + cosû , Y = sin û
C'est bien une équation de la tractrice lorsque a = 1.
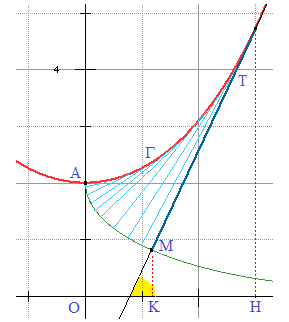
La tractrice
(en
rouge) est une développante de
chaînette
(en
bleu)
Développée de la tractrice : »