
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
@ tester le programme en ligne Tester le programme JavaScript , programme Basic , 10000 décimales de π | Autres calculs de π |
Il existe un très grand nombre de séries convergeant vers π. Beaucoup sont basées sur le développement en série de la fonction Arc tangente (Arctg ou Atan), série de Gregory :
D'où, puisque Atan(1) = π/4 :
Mais cette série converge très lentement et les erreurs d'arrondi s'accumulent car les termes sont de plus en plus faibles. Noter qu'en tant que série alternée, l'erreur ε est ici inférieure au premier terme négligé : ε < | un+1|. Ce qui montre que pour assurer une bonne précision, il faudra "pousser" les sommes assez loin...
On peut accélérer la convergence en regroupant les termes 2
par 2 mais ce procédé reste peu efficace. Une formule stable bien adaptée à la
programmation nous est donnée par :
![]()
Cette formule s'obtient par un procédé d'accélération de la convergence dû à Euler. Plus difficile à prouver, nous l'admettons ici. Elle peut s'écrire :

et le terme général de la série vn convergeant vers π vérifie alors vo = 2 et : vn = vn-1× n/(2n + 1).
Admettons, dans un premier temps, que nous
connaissions le rang nmax permettant d'atteindre 100 décimales
exactes au moyen de la série (s). Si nous apprenons à l'ordinateur à effectuer
une multiplication et une division à 100 décimales :
| L'organigramme suivant permet de calculer une approximation de π avec 99 décimales exactes : |
Condition initiale : Pi = 2n/(2n + 1) avec n = nmax
Programme : Tant que n ≥ 1
Diviser Pi par 2n - 1 (division à 100 décimales)
Multiplier Pi par n - 1 (multiplication à 100 décimales)
Ajouter 2 à Pi
Décrémenter n (on soustrait 1 à n)
Fin tant que.
| Stabilité de l'algorithme : |
Notons ek
l'erreur de troncature de l'ordinateur à l'itération k,
vu l'algorithme, on a : ek+1
< ek/2. On en déduit que
l'algorithme est stable (les erreurs de troncature ne se propagent
pas) et par conséquent que l'on obtiendra ainsi 99
décimales exactes de π,
la 100ème pouvant être arrondie par défaut
(penser que la dernière opération à 100
décimales est une multiplication par 2 : la retenue ne peut
excéder 1).
On en déduit que si l'on veut calculer
π à 10-N près, il faut
1/2n-2 < 10-N, condition
réalisée pour n = nmax tel que :
➔
Recherchons
dès lors la valeur de nmax : le dernier terme
négligé doit être inférieur à
10-N. Or :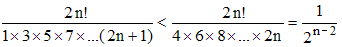
si N = 100 : nmax> 334 , si N = 1000 : nmax> 3324 , si N = 10 000 : nmax> 33221
La division à 100 décimales est étudiée et décrite pour le calcul de 100 décimales de e, il s'agit d'apprendre à faire maintenant les multiplications : le multiplicande Z possède 100 décimales, le multiplicateur est un entier "normal" m. Si B est la base utilisée (ici B = 10000), Z est de la forme :
Les Ti , i variant de 0 à 25, sont les chiffres (tranches à 4 chiffres en base 10) de notre système à base B. On effectue la multiplication par m de "droite" à "gauche" :
Tn devient Tnz que l'on écrit sous la forme B.q + r en effectuant une division euclidienne. Par suite, le dernier "chiffre" est maintenant Tn = r;
on repousse alors Bq dans BTn-1 qui devient B(Tn-1 + q);
Tn-1 + q est multiplié par m que l'on écrit sous la forme Bq' + r';
B(Tn-1 + q) devient alors B(Bq' + r') = B2q' + Br'. Par suite l'avant dernier "chiffre" Tn-1 est maintenant r'
Et ainsi de suite...
Le cas de la multiplication de To est particulier : il doit être multiplié par m et hériter du dernier quotient q. Un problème se poserait si un risque de dépassement pouvait exister : To ne doit pas dépasser B - 1. Concernant notre étude, il n'y a aucun risque puisque la convergence de notre série assure To ≤ 3.
| Le programme JavaScript : |
L'esprit du programme est très semblable à celui donné pour le calcul de 100 décimales de e. Compte tenu du risque d'erreur sur la 100ème décimale, nous calculons π sur 26 tranches décimales au lieu de 25 (en base 10000, on assure alors 104 décimales, la 104ème étant incertaine) et on n'affiche que 25 tranches. La tranche d'indice 0 contiendra, comme dans le calcul de e, la partie entière du quotient. On a ici nmax > 346.
➔ Le calcul est très rapide pour 100 ou 1000 décimales : 1 seconde, voire moins... A l'époque de Euler, il fallait quelques mois ! Dans le second cas, on choisit b = 100000 (pour aller un peu plus vite), nmax = 3340 et puisque 1000 = 200 × 5, il faudra prévoir 200 + 1 = 201 tranches.
|
<SCRIPT
LANGUAGE=JavaScript> for(i=1;i<=26;i++)
{T[i]=0} // on initialise les calculs : T(0)=2n, les autres tranches
sont nulles. aff=T[0].toString()+","
//
Pour l'affichage de l'approximation de Pi : on stocke les
function
divise()
//
sous-programme de division étudié dans le
calcul de 100 décimales de
e function
multiplie()
//
sous-programme de multiplication function go2()
// 1000
décimales |
oooOooo

» Programme
Basic équivalent , 10000 décimales
de π , autres
calculs , un calcul très précis
de e...
© Serge Mehl -
www.chronomath.com