ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Caustique par réflexion

Avez-vous remarqué au fond de votre tasse de café la jolie courbe qui se forme à la surface, d'autant plus visible que la lumière est rasante ? Après avoir lu l'étude ci-dessous, vous ne pourrez plus préparer votre petit déjeuner sans penser à l'épicycloïde, appelée aussi dans ce cas précis caustique (du grec kausticos = brûlant) d'un cercle par réflexion.

La tasse nécessaire à notre étude sera de forme cylindrique. Un rayon de lumière zM, supposé rasant la surface du liquide ou le fond de la tasse, tombe sur la paroi interne et est réfléchi suivant Mz'.

Le lumineux zM se réfléchit en Mz' en suivant la loi bien connue de la réflexion : on trace la normale (d) en M à la circonférence (perpendiculaire à la tangente, en pointillé sur la figure) : on obtient alors l'angle d'incidence ^(zM,d) = a (exprimé en radians). L'angle de réflexion étant égal à l'angle d'incidence, on repart en Mz' de sorte que (d) est bissectrice de l'angle ^zMz'. L'angle a peut varier de 0 (le rayon tombe en B et est réfléchi sur lui-même) à p/2 (le rayon tombe en A et continue sa route...).

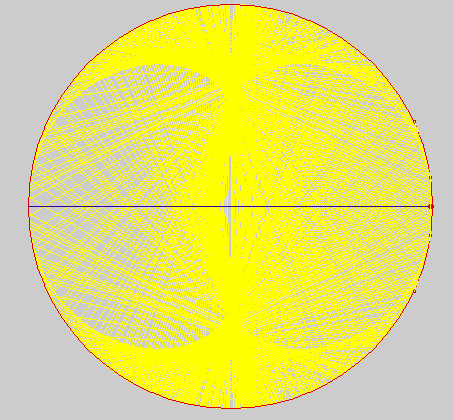
Le tracé de quelques rayons explique en partie l'allure de la courbe. Voici ce que fournit un ordinateur à qui l'on a fourni l'équation des rayons réfléchis que nous allons déterminer ci-après :

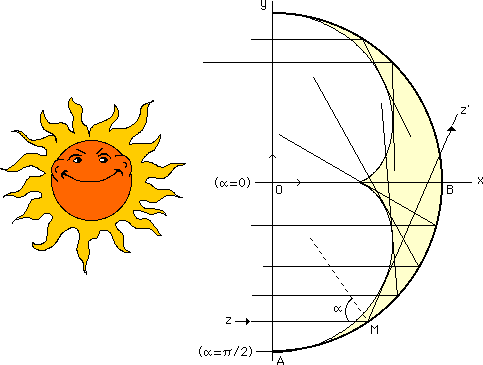
Définissons un repère orthonormé direct (Ox,Oy) comme indiqué (cf. ci-dessus). La courbe (C) cherchée admet manifestement (Ox) comme axe de symétrie. On peut se contenter d'étudier le phénomène dans le quadrant (AOB) et compléter par symétrie : en remarquant que la normale en un point d'une circonférence passe par le centre de celle-ci, on montre que le coefficient directeur de la droite réfléchie (Mz') est égal à tan 2a.

On note R le rayon de la tasse. Dans ces conditions, on montre facilement que :

• i/ M (Rcos a, Rsin a)
• ii/ Une équation de (Mz') est : x.sin2a - y.cos2a - R.sina = 0  (1)

Ainsi, (C) est l'enveloppe de toutes les droites (Mz') lorsque a varie de -p/2 à +p/2. Son équation est obtenue en dérivant (1) par rapport à a.

On remarque la concentration des droites vers le bord de la courbe et surtout à la pointe centrale
ce qui correspond à une concentration de lumière que l'on observe effectivement
 

Le système (s) obtenu :

x.sin 2a - y.cos 2a = R.sin a

2x.cos 2a + 2y.sin 2a = R.cos a

fournit facilement une équation paramétrique x = f(a) , y = g(a) de la caustique :

4x = R(3.cos a - cos 3a)

4y = R(3.sin a - sin 3a)

Une étude de x = f(a) et y = g(a) avec R = 6 conduit à la courbe ci-dessus. Noter que x est une fonction paire de a et y une fonction impaire : on se restreint donc à l'étude sur [0, +p/2]. f'(a) s'annule alors en +p/4 et x croît de 3 à 3 puis décroît jusqu'à 0. Dans ce même intervalle, y croît de 0 à 6.

 La courbe (C) complétée par symétrie par rapport à (Ox) et (Oy) est une épicycloïde, plus précisément néphroïde possédant deux points de rebroussement. La voici générée par Cabrijava :