
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
Considérons une série de lignes également espacées (par exemple les bandes d'un parquet bien lisse) et une aiguille ou une fine baguette bien équilibrée dont la longueur égale l'espacement entre les lignes. Lançons l'aiguille au hasard sur le parquet en notant 1 si l'aiguille rencontre une ligne et 0 sinon.
si, cas éminemment improbable, l'aiguille tombe perpendiculaire aux lignes et juste entre deux lignes, vous déciderez de compter 1 ou 0, en votre âme et conscience, ce cas marginal.
La figure ci-dessous schématise trois lignes d'espacement e et l'aiguille assimilé à un segment de milieu J, également de longueur e. Privilégions, pour l'étude, la seconde ligne L2.

On se propose d'évaluer la probabilité de l'événement E : « l'aiguille rencontre L2, J se trouvant entre L2 et L3 ». Notons :
• â l'angle des droites (JM)
et L2 : a∈[0,π];
• d la distance JH
: d∈[0,e]
L'aiguille ne rencontre L2 que si JM est inférieur à e/2, c'est à dire si d ≤ e/2 ×sin â.
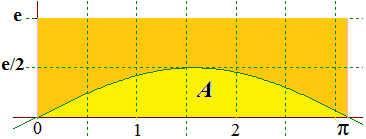
Selon le résultat 2 relatif aux méthodes de Monte Carlo, si on note A l'aire sous la courbe â → e/2 × sin â sur l'intervalle [0,π] représentée ci-dessus, on déduit que la probabilité p de l'événement E est A/πe avec :
C'est dire que p = 1/π. On obtient le même résultat si l'on suppose J entre L2 et L3.
En conclusion, la probabilité que l'aiguille coupe L2, ou tout autre ligne, est égale à 2/π
➔ Rappelons maintenant, en termes élémentaires, la loi faible des grands nombres de Jacques (Jakob) Bernoulli, que Buffon utilisa :
Si on répète un nombre N de fois une épreuve de Bernoulli, épreuve conduisant à deux éventualités, l'une appelée succès, de probabilité p et l'autre appelée échec, de probabilité 1-p, alors en notant F le nombre de succès au cours des N épruves, l'événement :
devient certain (sa probabilité tend vers 1) lorsque N tend vers l'infini.
On déduit de cette loi qu'il est hautement probable d'obtenir au bout d'un grand nombre de lancers N, une approximation F/N du nombre 2/π, donc une approximation N/F du nombre π/2.
| Expérimentation & programmation de la méthode en JavaScript : |
Tentez l'expérience pour au moins 200 lancers. Les résultats sont tout à fait grossiers pour prétendre calculer π mais tout à fait remarquables par la convergence dans l'intervalle [3,1 ; 3,2].
Ce petit programme vous propose 1000 lancers et vous permet, tout en faisant l'expérience, de contrôler la convergence vers π du rapport 2N/F : à la demande (0 ou 1) , si votre aiguille a coupé une ligne, vous entrerez 1 , sinon vous entrerez 0. Le programme affiche les résultats tous les 10 lancers.
Ne trichez surtout pas, laissez faire le hasard !
|
<SCRIPT
LANGUAGE=JavaScript> |
Des résultats partiels pour quelques 425 lancers authentiques :
| 0,5 | 0,66 | 0,75 | 1 | 1 | 1,2 | 1,16 | 1,14 | 1,28 | 1,25 | 1,37 |
| 1,33 | 1,30 | 1,40 | 1,50 | 1,60 | 1,54 | 1,63 | 1,72 | 1,81 | 1,75 | ... |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
...
|
| 3,12 | 3,08 | 3,1 | 3,12 | 3,14 | 3,16 | 3,18 | 3,20 | 3,22 | 3,17 | ... |
| 3,21 | 3,22 | 3,20 | 3,18 | 3,19 | 3,20 | 3,18 | 3,16 | 3,17 | 3,15 | 3,16 |
| 3,14 | ... | ... | ... |
et le graphique représentant les valeurs successives du rapport N/F, obtenu point par point. On voit après quelques oscillations, apparaître une convergence vers le célèbre nombre :