ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
Étude d'une fonction Arc sinus
niveau BTS/Bac+1 |
On considère la fonction f définie par :
où Asn désigne la fonction Arc sinus.
1°) On pose g(x) = Asn(sin(x)). Donner les différentes déterminations de g pour x variant de 0 à 2π.
2°) Utiliser 1°) afin de donner une définition par intervalles de la fonction f au moyen de la fonction Acs (» Arc cosinus). Pour ce faire, on posera provisoirement x = cosα, 0 ≤ α ≤ π.
3°) Calculer f '(x) et vérifier ainsi le résultat de 2°.
4°) Représenter les variations de f dans un repère orthonormé (on prendra 2 cm comme unité).
Si vous séchez après avoir bien cherché : ››››
Prolongement :
Étudier f(x) = Acs[2x/(1 + x2)] en posant cette fois dans des conditions que l'on précisera, x = tanα.
| Solution : |
1°) La fonction Arc sinus (Asin ou Asn) réalise une bijection de l'intervalle [-1;1] sur l'intervalle [-π/2,π/2]. La fonction g est continue; par translation, on se ramène dans [-π/2,π/2] en remarquant que sin x = sin(π - x) = sin(x - 2π). On peut alors dresser le tableau suivant pour x variant de 0 à 2π :
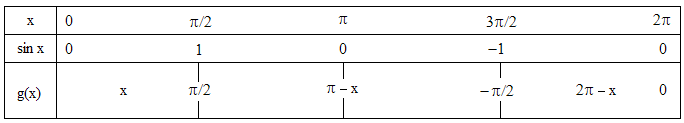
2°) En posant x = cosα, on a f(x) = Asn[2cosα√(1 - cos2α)] = Asn[2cosα|sinα|] = Asn(sin2α) car |sinα| ≥ 0 puisque est dans [0,π] ce qui fait varier x continûment dans l'ensemble de définition de f, à savoir [-1,+1]. On utilise le tableau pour conclure :
3°) On dérive f en tant que fonction du type Asn(u(x)). Un calcul relativement simple conduit à :
» L'écriture sgn z désigne la fonction signe égale à 1, 0 ou - 1 suivant que z est positif, nul ou négatif.
-1/√(1 - x2) est le nombre dérivé de Acs(x), fonction Arc cosinus, et compte tenu du signe de 2x2 - 1, on peut conclure que :
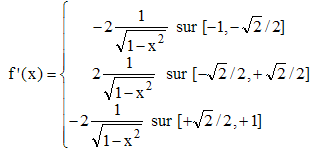
fonction dérivée de f, corrobore le résultat de 2°.
4°) On obtiendra sans difficulté la représentation par intervalles ci-dessous :
