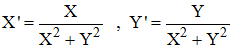ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 
inversion géométrique (plane) #3
niveau Sup ou TD niveau TerS» #1 (inverse d'un cercle) | #2 (étude analytique) | » construction de Napoléon |
On considère dans le plan euclidien (P) muni d'un repère orthonormé d'origine O, la transformation T qui, à tout point M d'affixe z = x + iy autre que i, associe le point M' d'affixe z' = x' + iy' tel que
1°/ Déterminer les points invariants par T. En déduire que T n'est pas une application affine.
2°/ Soit I le point d'affixe i. Prouver que I, M et M' sont alignés.
3°/ Prouver que IM.IM' = 1. Quelle est la nature géométrique de T ?
4°/ On se place dans le repère d'origine I. Montrer que l'expression analytique de f dans ce repère est :
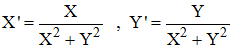
➔ On retrouve ici que l'inversion de pôle l'origine, de rapport 1 se traduit par la transformation z → z/|z2|
Si vous séchez après avoir bien cherché : ››››
| Solution : |
1°/ On recherche z tel que z = T(z). On passe en x ey y, ce qui conduit sans difficulté à
x2 + y2 - 2y = 0
soit à :
x2 + (y - 1)2 = 1
Il s'agit donc du cercle de centre ω(0,1) de rayon 1.
➔ On retrouve ici un résultat général concernant l'inversion géométrique, à savoir que l'ensemble des points invariants d'une inversion est un cercle (de centre le pôle de l'inversion, de rayon la racine carrée de sa puissance).
2°/ Il s'agit de prouver que les vecteurs IM et IM' sont colinéaires, donc que z' - i et z - i sont proportionnels dans un rapport k réel.
Or, un petit calcul conduit à z' - i = 1/(i + z). On multiplie et redivise le membre de droite par la quantité conjuguée de i + z, à savoir - i + z = z - i.
En posant kz = 1/|i + z|2 ∈ R+*, on obtient : z' - i = kz(z - i). En d'autres termes :
IM' = kz.IM
3°/ IM et IM' étant colinéaires et le calcul précédent montrant que k est strictement positif, on en déduit que le produit scalaire IM.IM' n'est autre que le produit IM.IM'.
On a IM(x,y - 1) et IM'(x/kz2,(y - 1)/kz2), soit :
IM.IM' = (x2 + (y - 1)2)/kz2 = 1 car i + z = x + i(1 - y).
4°/ En posant IM(X,Y), IM'(X',Y') et Z = z - i pour tout z de C, on a Z' = kzZ et Z = z - i conduit à i + z = Z, donc à kz = 1/| Z |2 = 1/| Z |2 = 1/(X2 + Y2). On a donc bien finalement :