
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
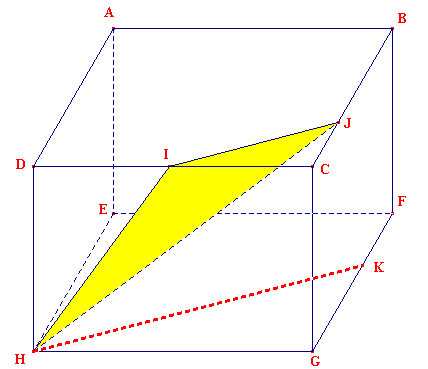
Voici une perspective d'un parallélépipède. Pour une meilleure interprétation en 3D, on peut supposer que c'est un pavé droit ou un cube mais cela n'a pas d'importance ici. On devra faire appel aux seules propriétés de plans et droites parallèles.
I est situé sur [DC], J est situé sur [BC].

1°) Construire, en justifiant, l'intersection du plan (IJH) avec la face EFGH.
2°) En déduire l'intersection du plan (IJH) avec le plan (ABFE). Justifier votre raisonnement.
3°) Construire, en justifiant, l'intersection du plan (IJH) la face ADHE.
| Réponse : |
1°) Le plan (IJH) contient le point H de la face EFGH. La droite (IJ) est située dans le plan (ABCD)parallèle au plan (EFGH). Par conséquent (IJH) coupe ce dernier plan suivant une droite parallèle à (IJ) passant par H. Cette parallèle coupe (FG) en K (la perspective cavalière conserve le parallélisme). L'intersection cherchée est le segment [HK].
➔ Si l'on place différemment les points I et J, il se peut que N soit un point de [EF].
2°) J et K sont deux points de la face CBFG. Par conséquent (IJH) coupe cette face selon [JK] (en vert). Traçons maintenant les demi-droites [IJ) et [HK) incluses toutes deux dans les plans (IJH).
[IJ) est incluse dans (ABCD) et coupe (AB) en L qui est un point du plan (ABFE);
[HK) est incluse dans (EFGH) et coupe (EF) en M qui est un point du plan (ABFE);
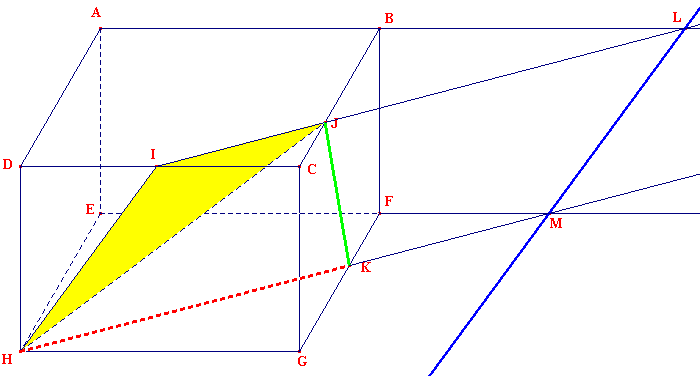
L'intersection cherchée de (IJH) avec (ABFE) est donc la droite (LM).
➔ On aurait pu également procéder en remarquant que (IH), droite du plan (IJH), est dans le plan (DCGH) parallèle à (ABFE). Par conséquent l'intersection du plan (IJH) avec (ABFE) est une droite parallèle à (IH). On prolonge alors [HK] en la demi-droite [HK) coupant (EF) en M et on trace la parallèle à (IH) passant par M.
3°) L'intersection du plan (IJH) la face ADHE contient H. il nous faut trouver un second point. Prolongeons [IJ] en la demi-droite [JI) incluse dans le plan (ABCD). elle coupe [AD) en N qui appartient donc tant à (IJH) que (ADHE). L'intersection cherchée est alors la droite (NH).

? On peut remarquer que (NH) semble parallèle à (JK). Justifie qu'il en est bien ainsi !