ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Constructions de triangles #2       niveau CM2/6è            » #1 , #3 , #4 , #5 à 10       Outils : compas, double décimètre

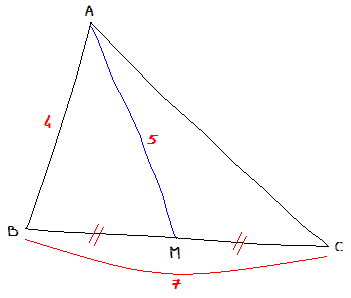
Écris le programme de construction du triangle ABC dessiné ci-dessous "à main levée", puis construis-le avec soin (le codage indique que M est le milieu de [BC]) :

Si tu sèches après avoir bien cherché : ››››

• Tracer un segment [BC] de mesure 7 cm;

• Placer le milieu M de [BC]   (BM = BC = 3,5 cm);

• Tracer un arc de cercle de centre M de rayon 4 cm;

• Tracer un arc de cercle de centre B de rayon 5 cm;

• On note A l'intersection des deux arcs;

• Tracer [AB] et [AC].

- o0o -

Remarque niveau collège :

Le triangle ABM est constructible puisque ses côtés de mesures 5, 4 et 3,5 vérifient l'inégalité triangulaire; le triangle ABC est alors déterminé à une symétrie près : symétrie axiale par rapport à (BC).

- o0o -

En toute rigueur... :

Toute construction doit être conduite par analyse et synthèse. L'analyse est le raisonnement aboutissant à la construction cherchée. Mais le processus d'analyse procède par implication : si ABC existe (on suppose la construction aboutie) alors on a nécessairement (forcément en langage élève) ceci ou cela, donc on va faire ceci ou cela.

La synthèse consiste à vérifier que ces conditions nécessaires aboutissant à la construction sont aussi suffisantes, c'est à dire que cette construction vérifie bien toutes les hypothèses de l'énoncé.