
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
» Tangente au cercle (rappels des propriétés) niveau : a1, a2, a3) TD 4ème | autres cas : oral concours... |
On considère deux droites d1 et d2 d'un plan et un cercle (c) de centre O. On s'intéresse au problème consistant à construire un cercle (au moins) tangent à ces deux droites et à ce cercle. Les outils autorisés sont règle non graduée, compas, équerre à la manière d'Euclide. On considérera deux cas :
a) les droites sont parallèles comme figurées ci-dessous : six cas peuvent avoir lieu, le 1er (en rouge) est à rejeter. Les second et troisième cas sont simples.

b) les droites sont sécantes en O comme figurées ci-dessous. On appellera A le centre du cercle et on se ramènera au cas PDD de la construction d'un cercle passant par un point (A) et tangent à deux droites :

En observant cette figure tracée approximativement avec l'aide du logiciel CabriGéo afin d'analyser la situation, on comprend qu'il y aura 4 solutions : deux cercles tangents extérieurement (en rouge) et deux autres tangents intérieurement (en vert) :

Si vous séchez après avoir bien cherché... : ››››
| Solution : |
a1) Les droites d1 et d2 étant parallèles, le cercle ne peut pas être situé "entièrement" à l'extérieur de la bande limitée par les deux parallèles. Dans ces conditions, le premier cas (cercle extérieur à la bande, représenté en rouge dans la figure énumérative de l'énoncé) est à rejeter.
a2) Le cercle (c) est tangent extérieurement en K à l'une des deux droites (figure ci-dessous) : dans ce cas (OK) est perpendiculaire aux deux droites. L'unique solution est le cercle dont le centre O1 est situé sur (OK) à égale distance de d1 et d2 :

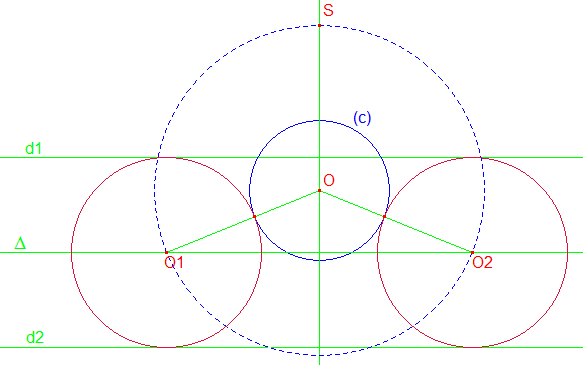
a3) Le cercle (c), de centre O, est tangent intérieurement aux deux droites en A et B. [AB] est un diamètre du cercle (c), perpendiculaire aux deux droites (figure ci-dessous). On trace la parallèle Δ aux droites d1 et d2 passant par O. Les deux cercles centrés sur Δ en O1 et O2, tangents extérieurement à (c) et de même rayon que ce dernier répondent à la question.

➔ Collégiens : Dans ce problème de construction, le double-décimètre n'est pas autorisé. Lorsque l'on dit "de même rayon", cela ne signifie nullement que l'on mesure ce rayon au moyen d'une règle graduée : il s'agit ici de reporter cette prise de mesure grâce au compas : on pique le compas en O et on l'écarte jusqu'à la circonférence du cercle (c). Avec cet écartement, on trace les cercles de centre O1 et O2.
a4) On suppose ici que (c), figuré en bleu ci-dessous, est tangent intérieurement à d1 en J, de rayon OJ = r. Ce cercle étant intérieur à la bande définie par d1 et d2, les cercles cherchés devront l'être également. Comme dans le cas précédent, devant être tangents à d1 et d2, ces cercles, ont même rayon R (demi-distance entre d1 et d2) et seront donc centrés sur Δ parallèle à d1 et d2. Une solution apparait immédiatement : cercle de centre O1 passant par J tangent intérieurement à (c).

Si un cercle (s) de centre O2 est solution et tangent extérieurement à (c) en K, alors O, K et O2 sont alignés et OO2 = r + R. D'où la construction : soit S le symétrique de O1 par rapport à J. On a OS = r + R. Le cercle de centre O passant par S (en pointillés bleu) coupe Δ en O2 et O3. Les cercles de centre O1 et O2 de rayon R répondent manifestement à la question.
a5) On suppose ici que (c) est intérieur à la bande définie par les parallèles d1 et d2. Si un cercle de centre O1 est candidat tangent extérieurement à (c), son rayon est R (demi-distance entre d1 et d2) et comme précédemment, OO2 = r + R. On est amené à la construction précédente construisant S sur la perpendiculaire commune à d1 et d2 passant par O tel que OS = r + R. Pour cela, on reporte au moyen du compas la demi-distance R à partir de J et on obtient deux solutions symétriques par rapport à (OS).

Mais on soupçonne l'existence de deux solutions où (c) est tangent intérieurement aux cercles cherchés. Le processus de construction est semblable au cas précédent en procédant par soustraction... :

a6) Semblable au cas a4 avec perte du cercle tangent intérieurement :
b/ Les droites sont sécantes en un point O :
R désignant le rayon du cercle donné (c), traçons deux droites auxiliaires (O'x') et (O'y') intérieures à l'angle xOy, sécantes en O' sur la bissectrice (Oz) de l'angle ^xOy et tracées parallèlement aux droites d1 et d2 à la distance R de ces droites. On utilise alors la construction PDD afin de construire les deux cercles de centre O1 et O2 passant par A et tangents à (O'x') et (O'y'). On obtient ensuite les deux cercles tangents extérieurement en ajoutant R (par report du compas) aux rayons des cercles obtenus :

Afin d'obtenir les deux cercles tangents intérieurement, on utilise encore la construction PDD en utilisant cette fois deux droites auxiliaires ('Ox') et ('Oy') extérieures à l'angle xOy, tracées parallèlement aux droites d1 et d2 à la distance R des de ces droites. On obtient ensuite les deux cercles tangents intérieurement en soustrayant R (par report du compas) aux rayons des cercles obtenus :
