ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Théorème de Rouché-Fontené       » exemple d'application

Considérons et appelons (s) le système n x p de n équations linéaires à p inconnues x₁, x₂,…,x_p :

a_1,1x₁ + a_1,2x₂ + … + a_1,px_p = b₁
a_2,1x₁ + a_2,2x₂ + … + a_2,px_p = b₂
…
...
a_n,1x₁ + a_n,2x₂ + … + a_n,px_p = b_n

où les a_i,j et les b_i sont des réels donnés, 1 ≤ i ≤ n, et 1 ≤ j ≤ p.

• le système (s) peut s'écrire matriciellement Ax = b où A = (a_i,j) est la matrice du système, x est la matrice colonne des x_i, b la matrice colonne des b_i et s'interprète comme une équation de la forme f(x) = b où f est l'application linéaire d'un espace vectoriel E de dimension p vers un espace vectoriel F de dimension n.

• Il n'y a des solutions que si et seulement si b appartient à Imf = f(E), image de E par F.

• On appelle rang du système (s) la dimension du sous-espace vectoriel engendré par les vecteurs colonnes de A; c'est la dimension de Imf; c'est aussi le rang de la matrice A : nombre égal à l'ordre maximum d'un déterminant non nul extrait de A.

Soit D_r un déterminant d'ordre r non nul extrait de A; le rang de A est alors au moins égal à r.

On appelle déterminant bordant de D_r, ou tout simplement bordant de D_r, tout déterminant d'ordre r + 1 extrait de A dont D_r est un déterminant extrait. Il y a (n - r)(n - p) bordants.

La matrice A sera de rang r si et seulement si tous les bordants de D_r sont nuls.

∗∗∗ Un exemple :

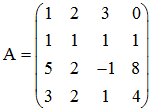
Le déterminant de A est nul; sans le calculer, on peut s'en persuader en remarquant par exemple que la seconde ligne est le quart de la somme des 1ère et 4ème ligne : L1 = ¼(L1 + L4).

 i   Plutôt que celle des lignes, on peut aussi constater la non indépendance des colonnes  : par exemple C4 = 2C1 - C2.

 Le déterminant 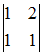 étant clairement non nul, A est de rang 2 ou 3. 

Les quatre bordants de ce déterminant sont :

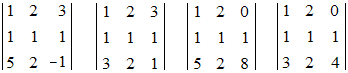
Et on peut vérifier qu'ils sont tous nuls : A est donc de rang 2.

Revenons à notre système (s) :  

• On a évidemment r ≤ p et, quitte à renuméroter, on peut supposer que le déterminant non nul d'ordre r extrait de A est constitué des r premières inconnues et équations. Ces inconnues et équations sont dites principales.

• Dans ce réarrangement, les r premiers vecteurs colonnes de A constituent une base de Imf, c'est dire qu'il n'y a de solutions que si le système de r + 1 vecteurs constitué de b et de ces vecteurs colonnes est lié : tous les déterminants bordants d'ordre r + 1, appelés déterminants caractéristiques du système, doivent être nuls (on en compte n - r). Ils sont de la forme :

   ,  i = r + 1, r + 2, ..., n

Si n = p, la matrice A est carrée et selon un résultat de Gabriel Cramer, le système admet une unique solution si le déterminant de A, déterminant du système, est non nul. Dans les autres cas, nous avons ce résultat fort utile dans la pratique :

Théorème de Rouché-Fontené :    

• si r = n : on a r inconnues principales (et n ≤ p); on peut donner aux autres des valeurs arbitraires (on les considère comme des paramètres, indétermination d'ordre p - r) et la résolution du système se ramène à un système de Cramer r × r;

• si r < n : si l'un des n - r déterminants caractéristiques de (s) est non nul, alors (s) n'a pas de solutions, sinon on est ramené au cas précédent.

∗∗∗  
Résolution d'un système de 4 équations à 3 inconnues

Considérons le système de 4 × 3 (4 équations à 3 inconnues) défini par :

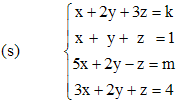    La matrice du système est :  

Son rang est 2 : on peut le calculer en étudiant les déterminants extraits d'ordre 3 (ils sont tous nuls) ou en constatant que la troisième colonne est le double de la seconde diminué de la première. On peut choisir comme équations (resp. inconnues) principales les deux premières équations (resp. x et y) puisque ces équations ne sont pas proportionnelles :

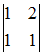= - 1 ≠ 0

Le système aura des solutions si et seulement si les deux bordants :

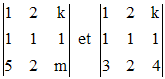
sont nuls, c'est à dire si et seulement si : 3k + m = 8  et  k = 0, soit finalement si et seulement si k = 0 et m = 8. Le système se réduit alors à : x + 2y = - 3z  et  x + y = 1 - z. En conclusion :

si k = 0 et m = 8, z est arbitraire, x = z + 2, y = -2z - 1, sinon pas de solution.