ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 
Un exemple de rectification : longueur d'un arc de parabole |
Une intégrale contenant une expression algébrique sous un radical, comme une racine carrée, est souvent difficile à calculer : on risque de tomber sur une intégrale elliptique...
Nous calculons ici la longueur de l'arc de parabole y = x2 lorsque x décrit l'intervalle [0,1]. A priori, cela paraît tranquille... On constatera pourtant que si l'équation de la courbe est simple, il n'en est pas de même de la longueur L d'un de ses arcs. Allons-y :
On a ici y'2 = 4x2 et par suite :
En intégrant par parties, calculons une primitive F de la fonction :
On obtient aisément :
En ajoutant et retranchant 1 au numérateur de l'intégrande, on a :
➔ Cette dernière primitive est connue car : son intégrande n'est autre que la fonction dérivée de la fonction réciproque du sinus hyperbolique, à savoir Arg sh x. C'est dire que l'on a :
L'expression de Arg sh x est facilement calculable :
Ainsi, à une constante additive près :
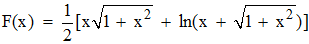
On revient alors à L , avec u = 2x :
Par suite :
L = [ F(2) - F(0)] / 2 = F(2) / 2 = [2√5 + ln (2+√5)] / 4 , soit L = 1,48 à 0,01 près. ouf !..