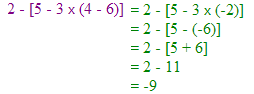ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
|
|
➔ On suppose ici connues les règles de suppression des parenthèses dans un calcul "en chaîne" ne contenant que des additions et/ou des soustractions. Il s'agit ici d'ajouter la présence de multiplications et, accessoirement, quelques divisions :
! Rappelons que dans un calcul en chaîne, la multiplication et la division sont prioritaires sur l'addition et la soustraction, c'est à dire qu'elles doivent être calculées avant les additions et soustractions. Cette convention permet d'éviter des parenthèses alourdissant les écritures.
Petit détour historique : »
| La fameuse règle des signes... : |
Supposons que ♦ et ♣ désignent des nombres arithmétiques (non signés) comme 2 ou 7,23. La règle des signes pour la multiplication peut se résumer ainsi :
(+ ♦)
x (+
♣)
=
+
♦
x
♣
et (-
♦)
x (-
♣)
=
+
♦
x
♣
Exemples : (+2) × (+5) = +10 , (-2) × (-5) = +10 , 11 - (-2) × (-5) = +1
(+ ♦)
x (-
♣) =
- ♦
x
♣
et (-
♦)
x (+
♣) =
-
♦
x
♣
Exemples
:
(+2) × (-5) = -10 , (-2)
x (+5) = -10 , 11 - (-2) x
(+5) = +21
➔ La même règle s'applique à la division. En résumé :
si a et b ont même signe, a ÷ b est positif , si a et b ont même signe, a ÷ b est négatif
On se limite, sur cette page, aux calculs comportant des additions, des soustractions, des multiplications et, accessoirement, quelques divisions.
|
Règle de priorité des parenthèses
: si des
opérations apparaissent dans une parenthèse, elles doivent être effectuées
en priorité. Parenthèses imbriquées : On appelle ainsi des parenthèses à l'intérieur d'une parenthèse, la priorité s'applique à la plus « intérieure ». Pour une meilleure lecture, on utilise des crochets.
Par exemple :
∗∗∗ Des exemples ∗∗∗ |

Et maintenant, entraîne-toi ! Les nombres affichés sont entiers pour éviter les
tracas de calcul, l'objectif étant ici de maîtriser la règle des signes et la
suppression des parenthèses.
![]() La calculatrice est bien sûr interdite !!!
La calculatrice est bien sûr interdite !!!
![]()

Mais un crayon et une feuille de brouillon sont souhaitables
!
Ne pas mettre d'espaces entre
les signes et les nombres
!
On peut obtenir la réponse sans rien écrire :
cliquez sur OK
Élèves, professeurs, internautes, merci de me signaler tout dysfonctionnement dans ces programmes

On évite ici signe l'insupportable "deux points" (:) de Leibniz, vieux relent encore en usage à l'école primaire (et dans les sujets de Brevet...) et piège pour les élèves, à la limite de la préméditation..., conduisant inéluctablement à des erreurs tant de lecture que d'interprétation (confusion entre signe typographique et codage mathématique). Dans un calcul en chaîne, dès la classe de 5ème, la division ne devrait d'ailleurs apparaître que par le truchement de l'écriture fractionnaire :
![]() » Oresme
» Oresme
Quel est donc l'objectif de l'usage persistant de ces écritures autant désuètes que pénalisantes ?
© Serge Mehl - www.chronomath.com