ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 |
 Section d'une pyramide
par un plan
niveau
2nde
» section d'un tétraèdre , section d'un cube , voir aussi (niveau seconde) |
Voici un tétraèdre SABC. On a placé trois points sur ses arêtes : K sur [SA], L sur [SB] et M sur [BC] :
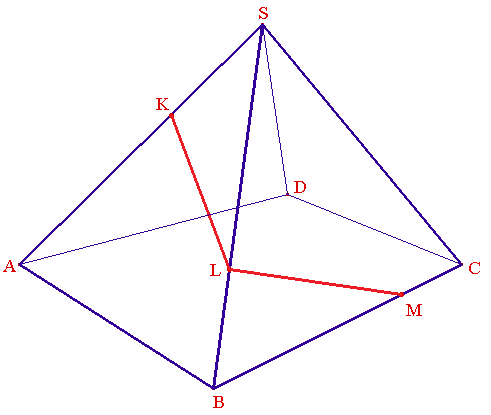
➔ Si votre navigateur le permet, voici la même figure générée par Cabri Géomètre dans sa version CabriJava pour Internet :
Si votre navigateur accepte les applets Java
(»
extension CheerpJ
) :
Vous pouvez
changer le point de vue ou réduire/agrandir en déplaçant S, A, B ou D
On suppose (KL) et (AB) sécantes en I et (LM) et (SC) sécantes en J. On demande de représenter la section de la pyramide SABCD par le plan (KLM)
Si vous séchez après avoir bien cherché : ››››
| Solution : |
Il s'agit de construire les traces du plan KLM sur chaque face de la pyramide.
On connaît déjà [KL] sur (SAB) et (LM) sur (SBC). Reste donc à connaître deux traces : sur (ABCD), (SDC) et (SAD).
[KL) coupe [AB) en I : c'est un
point de (KLM) et de (ABCD).
Mais M en est un autre : [IM) coupe alors
[DC] en P.
Le segment [MP] est la trace cherchée sur (ABCD);
[LM) coupe [SC) en J : J et P
sont deux points de la trace sur (SDC);
La droite (JP) est incluse dans (KLM);
soit Q l'intersection de (JP) avec [SD];
Les traces de (KLM) avec (SDC) et
(SAD) sont alors respectivement [PQ] et [KQ];
Finalement, la section de la pyramide par le plan (KLM) est le pentagone KLMPQ.
Si votre navigateur accepte les applets Java
(»
extension CheerpJ) :
Vous pouvez
changer le point de vue ou réduire/agrandir en déplaçant S, A, B ou D