ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 Taux d'intérêt
simple
#2
TD niveau 2nde/1ère
»
variante
»
notion de pourcentage» intérêts simples ou composés Outils : notion de taux d'intérêt, équation du second degré ou forme canonique du trinôme |
Cette histoire se passe dans les années 1970-1980 à une époque où l'inflation très élevée voyait aussi l'avènement de taux d'intérêt pouvant dépasser les 10% !
Une personne a placé un capital de 10000 € à un taux initial t% que vous devez calculer sachant que :
♦ La personne a d'abord placé les 10000 € à t% pendant six mois.♦ La valeur alors acquise (capital + intérêt) a été placée à un taux plus rémunérateur : 4% de plus et ce pendant dix-huit mois à intérêts simples.
♦ à la fin de la seconde période les intérêts acquis (au total sur les 2 ans) s'élevaient à 2205 €.
➔ Un taux s'exprime en pourcentages. Par exemple, dire que l'on place une somme d'argent à 3% (3 pour cent) signifie que 100 euros rapporte 3 € en un an. Un taux de deux points supérieur signifierait dans ce cas un taux de 5% (3 + 2).
| Solution : |
Les 10000 € placés pendant 6 mois (une demi-année) rapportent en euros :
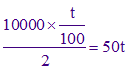
18 mois représentent 1,5 année. La valeur acquise, soit 10000 + 50t, rapporte alors :
On est ainsi amené à résoudre l'équation : 1,5 × (10 000 + 50t)(t + 4)/100 = 2205, soit (10 000 + 50t)(t + 4) = 147000.
Il s'agit d'une équation du second degré qui se ramène à :
t2 + 204t - 2140 = 0
La solution cherchée doit être positive. En classe de 1ère, vous trouverez facilement t = 10 en résolvant cette équation. Le taux cherché est donc 10%.
➔ En classe de seconde, on pourra utiliser la forme canonique du trinôme. On peut écrire :
t2 + 204t - 2140 = (t + 102)2 - 1022- 2140 = (t + 102)2 - 12544 = (t + 102)2 - 1122
L'équation se ramène donc à : (t + 102)2 = 1122, ce qui équivaut à t + 102 = ± 112. D'où t = 112 - 102 = 10 ou bien t = -112 - 102. Cette dernière possibilité négative est à rejeter : le taux cherché est 10%.