ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Équation différentielle linéaire du 1er ordre à coefficients variables    » plus simple     (oral École Centrale)

On considère l'équation différentielle du 1er ordre :

,   -1 < x < 1        

1°/ Résoudre l'équation sans second membre. Mettre la solution trouvée sous la forme :

2°/ En utilisant la méthode de la variation de la constante, vérifier que :

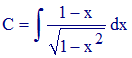
3°/ En déduire la solution générale de l'équation donnée.  » fonction Arc sinus.

1°/ Sur tout intervalle J sur lequel y ne s'annule pas, on peut écrire y'/y = 1/(1 - x²) = ½[1/(1 + x) + 1/(1 - x)]. Par conséquent, en remarquant que sur l'intervalle d'étude (1 + x)/(1 - x) est strictement positif, avec k₁ arbitraire et k₂ strictement positif :

En posant C = ± k2 (donc C arbitraire non nul), on obtient finalement la forme demandée :

2°/ Dérivons l'expression de y en supposant C fonction de x :

On reporte l'expression de y' dans l'équation initiale. Après simplification, il reste simplement :

3°/ En décomposant en différence de deux intégrales, on obtient immédiatement, avec k arbitraire :

Et la solution générale de l'équation initiale est alors, pour tout x de ]-1+1[ :