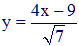ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Calcul des éléments caractéristiques d'une hyperbole   niveau Ter       » cas de l'ellipse , cas de la parabole

Vous pouvez contempler ci-dessous une belle hyperbole dont l'équation réduite est de la forme

x²/a² - y²/b² = 1

Au vu des indications fournies sur le graphique, on demande de calculer :

• a et b;   le fait que a semble égal à 3 n'est peut-être que le fruit de votre imprécision...

• c, abscisse du foyer F;

• e, excentricité;

• l'équation de l'autre asymptote;

• les équations des directrices;

• son paramètre p;

• l'équation exacte de la tangente en M sachant que son abscisse est 4.

  Si vous séchez après avoir bien cherché... : ››››

---

© Serge Mehl - www.chronomath.com

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Solution :

• a et b : la courbe passe par A(5,3), donc 25/a² - 9/b² = 1. Les asymptotes ont pour équations y = ± bx/a. on a donc ici b/a = 3/4, soit b = 3a/4. En remplaçant dans la 1ère équation, il vient 9/a² = 1. Le paramètre a étant positif, il apparaît donc que a = 3, puis b = 9/4.

x²/9 - 16y²/81 = 1

• c, abscisse du foyer F : c² = a² + b² fournit c = 15/4 = 3,75.

• e, excentricité : e = c/a = 5/4 = 1,25.

• l'équation de l'autre asymptote : y = -3x/4

• les équations des directrices : x = ± a²/c = ± 12/5 = ±2,4.

• son paramètre p : c'est la demi-corde passant par F, donc ici l'ordonnée du point M de l'hyperbole d'abscisse 15/4

. Un calcul fractionnaire fournit p = 27/16 = 1,6875.

• l'équation de la tangente en M sachant que son abscisse est 4 : l'équation en M(x_o,y_o) est xx_o/a² - yy_o/b² = 1 (» tangente aux coniques). En x_o = 4, on a y_o = 9√7/16. Pas très sympa cette valeur, mais bon, ça s'arrange un peu car on obtient finalement : 4x - y√7 = 9 ou, si on préfère :