ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 
Point de Fermat-Torricelli
solution géométrique
»
solution mécanique |
On considère un triangle ABC dont aucun angle n'égale ou ne surpasse 120°. Soit M un point intérieur au triangle ABC. Où doit se trouver M afin que la somme de ses distances aux trois sommets du triangle, c'est à dire MA + MB + MC, soit minimale ?
➔ On démontre que si un angle, ^A par exemple, mesure ou surpasse 120°, alors le point cherché est en A. On se propose d'apporter ici une solution partielle de ce problème utilisant une propriété remarquable de la normale en un point d'une ellipse.
♦ En s'aidant de la figure ci-dessous, on montrera facilement que si le problème de Fermat possède une solution, elle ne peut être extérieure au triangle ABC : c'est à dire qu'elle est située soit à l'intérieur du triangle ABC, soit sur son pourtour.
♦ Soit M une solution éventuelle. Il est situé sur une ellipse (e) de foyers B et C dont l'intérieur ne contient pas A. Sur cette ellipse la somme MB + MC est constante et MA + MB + MC sera alors minimum si MA est minimum, donc si (MA) est la normale (n) en M à l'ellipse : perpendiculaire à la tangente (t) au point M.
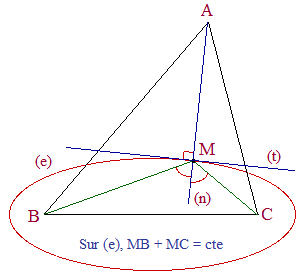
♦ Or, on sait (théorème de Poncelet) que la normale en M est bissectrice intérieure de l'angle ^BMC. Dans ces conditions :
♦ En raisonnant de même sur les côtés [AB] et [AC], on déduit des considérations ci-dessus que si le point cherché I existe, il vérifie :
^BIC = ^CIA = ^AIB = 120°
➔ Un tel point I est géométriquement constructible : point de Fermat du triangle. La question porte alors sur l'unicité : soit f la fonction qui à tout point M associe le nombre MA + MB + MC :
Supposer qu'il existe (au moins) deux points I et J minimisant cette fonction f. Noter O le milieu de [IJ].
Comparer AI + AJ, BI + BJ et CI + CJ aux distances respectives 2AO, 2B0 et 2CO.
Remarquer que l'une au moins des inégalités trouvées est stricte : sinon A, B et C seraient alignés sur (EF).
Déduire de ces
considérations, en calculant 2(OA + OB + OC), que O serait un
"meilleur" point que I et J :
f(O) < f(I) et f(O) < f(J).
Conclure.
Le problème admet intuitivement une solution mais la preuve de cette existence n'est pas simple. En mathématiques supérieures, on le prouve très simplement en remarquant que la fonction f : M → MA + MB + MC est continue sur la partie compacte constituée de l'intérieur du triangle et de sa frontière et qu'elle admet donc un minimum sur cette partie.
➔ Pour en savoir plus :
par
Yvonne et René Sortais.