ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
Courbe du diable |
Cette courbe algébrique (cubique) fut étudiée pour la première fois par Gabriel Cramer en 1750 dans son traité sur les courbes algébriques : Introduction à l'analyse des lignes courbes algébriques (» réf.1). Qualifiée de courbe du diable au 20è siècle, elle n'a rien de diabolique mais le "papillon" central rappelle le diabolo. Il s'agit d'une courbe algébrique du 4ème degré (quartique). Comme on le voit ci-dessous, Cramer choisit l'équation de cette quartique comme étant :
y4 - 96y2 - x4 + 100x2 = 0
Diabolo sur Wikipedia,
ou sur
YouTube :
https://www.youtube.com/watch?v=jLz3w459Ukw
pages 18-19
page 38 - fig. 12 ; y4 - 96y2 - x4
+ 100x2 = 0.
Remarquer la précision du graphisme !
Plus généralement, ce type de courbe correspond à une équation du type :
x4 - a2x2 = y4 - b2y2
Nous choisissons à l'instar de Gabriel Cramer :
y4 - 96y2 - x4 + 100x2 = 0 (e1)
comme équation de la courbe du diable que nous noterons (D).
Mais le logiciel Graphmatica refuse obstinément de tracer le branches infinies de la courbe donnée sous cette forme implicite initiale du 4ème degré (trop de calculs). Posons alors Y = y2. Nous obtenons Y2 - 96Y - x4 + 100x2 = 0, équation du second degré en Y. Un calcul élémentaire conduit à :
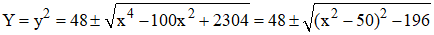
Mais 196 = 142. Finalement :
(e2)
Graphmatica sait tracer des familles de courbes. Le signe ± est remplacé ci-dessous par le paramètre multiplicatif a qui prendra les valeurs -1 et 1 : le 2 dans l'accolade indique le pas de variation de a.
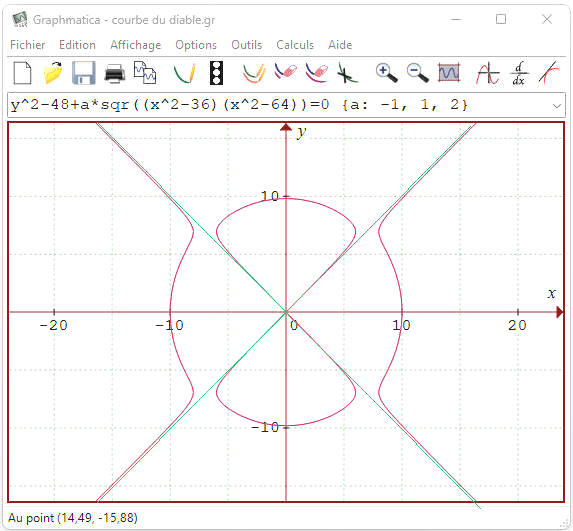
L'équation de la courbe sous la forme (e1) montre que les changement de x en -x et/ou de y en -y la laisse inchangée : l'origine est le centre de symétrie de la courbe. On peut donc étudier la courbe dans le 1er quadrant du repère x ≥ 0, y ≥ 0. Dans ce quadrant le produit (x2 - 36)(x2 - 64) est du signe de (x - 6)(x - 8), donc positif ou nul pour x ∈ [0,6] ∪ [8,+∞[.
En dérivant l'équation (e2) par rapport à x, nous obtenons :
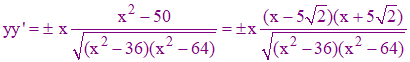
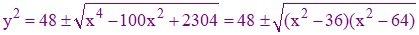(e2)
Avec les notations de (e2) ci-dessus, on note y2+ la détermination de y2 avec le signe + devant le radical et y2- celle obtenue avec le signe - :
Sur l'intervalle [0,6] : x - 5√2 est
négatif : y2+ décroît de √96 = 4√6 ≈ 9,8 à √48 = 4√3 ≈ 6,93
et y2-
croît de 0 à √48 = 4√3.
Par symétrie par rapport à l'axe des ordonnées, on obtient le "demi-diabolo"
supérieur, puis le diabolo dans son entièreté en symétrisant par rapport à
l'axe de abscisses.
Sur l'intervalle [8,+∞[ : x - 5√2 est
positif : y2+ croît de √48 = 4√3 à l'infini et y2- décroît de
√48 = 4√3 à 0 (en x = 10).
Par symétrie par rapport à l'axe des abscisses, on obtiendra la branche
infinie d'ordonnée négative et on complète finalement la courbe (D)
par symétrie par rapport à l'axe des ordonnées.
Nature des branches infinies : Considérons le rapport m = y2+/x2. On a :
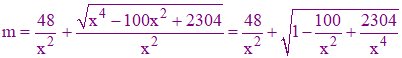
rapport qui tend manifestement vers 1 pour x infini. Globalement, nous avons là quatre branches infinies de directions asymptotiques les bissectrices du repère. En restant dans le 1er quadrant, recherchons alors la limite de y+ - x :
La courbe (D) admet donc les bissectrices du repère (tracées en vert) comme asymptotes obliques pour x infini (dans les 1er et 2ème quadrants la courbe est en dessous de son asymptote).
En coordonnées polaires,
en posant x = r.cos
t,
y = r.sint
dans l'équation (e1), on obtient facilement l'équation polaire de la courbe du
diable (on remarquera que cos2t - sin2t = cos4t
- sin4t) :
r2cos2t = 96cos2t + 4cos2t
Et la courbe s'obtient entièrement sur [0,2π] par :
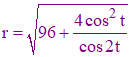
➔ Pour en savoir plus :
