
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
On étudie ici la notion de courbe de poursuite. Elle fut étudiée par Pierre Bouguer (à qui l'on doit le nom) et son contemporain et ami Maupertuis. On parle aussi de trajectoire d'interception et de courbe du chien.
On peut aussi penser de nos jours à un missile sol-air à tête chercheuse, dont l'ordinateur de bord calcule la trajectoire nécessaire à l'interception de la cible, au chien voyant passer une voiture et cherchant à la rattraper ou encore, comme illustré ci-dessous, à ce malheureux enfant, entrant par imprudence dans l'enclos du bélier.

i Pierre Bouguer : physicien, astronome et mathématicien français, 1698-1758. Membre de l'Académie royale des sciences. ll fut un spécialiste des problèmes de navigation et participa, au Pérou, avec La Condamine et Clairaut à la mesure des méridiennes terrestres (» Maupertuis). Dans un mémoire sur l'inclinaison des orbites des planètes (1734), il semble être le premier à utiliser les signes inférieur ou égal ≤ et supérieur ou égal ≥.
Schématisons cette situation :
L'enfant court suivant Oy (palissade) en direction de la maison; au départ il est en O et le bélier en B à 100 m de O. Ce dernier cherche à le rattraper : c'est dire qu'à chaque instant t, si M(x,y) désigne sa position et E celle de l'enfant, la tangente à la trajectoire du bélier est (ME).

Les vitesses, supposées constantes, de l'enfant et du bélier sont notées respectivement a et b. La position de l'enfant est donc régie sur Oy par :
OE = a × t.
♦ On note y = f(x) l'équation de la trajectoire du bélier. Le coefficient directeur de la tangente (ME) au point M est alors :
![]() , soit :
, soit :
x et y = f(x) sont des fonctions du temps t. Il s'agit alors d'éliminer le temps dans l'équation différentielle (e1). Différentions les deux membres par rapport à t :
dy/dt - a = y'.dx/dt + x.dy'/dt
Or :
![]()
d'où :
![]()
♦ Sur sa trajectoire, dans le temps dt, le bélier progresse d'une distance dl = b × dt; mais dl2 = dx2 + dy2 et par suite :
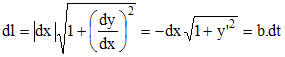 »
longueur d'un arc de courbe
»
longueur d'un arc de courbe| dx | = -dx car sur la trajectoire de M et selon nos hypothèses, x est positif et diminue (tend vers 0). Cette relation permet d'éliminer le temps dans (e2) en exprimant dx/dt. On obtient alors :
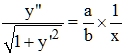
avec y' = y = 0 pour x = 1 (on prend l'hectomètre comme unité). En posant z = y', on a y" = dy'/dx = dz/dx. D'où, en séparant les variables :
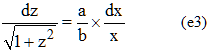
L'intégrale du membre de gauche n'est autre que Argsh z (fonction réciproque du sinus hyperbolique) à une constante additive près :
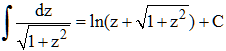
♦ On suppose maintenant que le bélier est deux fois plus rapide que l'enfant. On a donc b = 2a et a/b = 1/2. (e3) fournit alors :
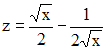 puis :
puis :
![]()
Dans ce cas le bélier rattrape l'enfant en y = 2/3 (soit à 67 m environ de O, courbe rouge).

♦ On suppose ici que le bélier et l'enfant courent à la même vitesse (a = b). On obtient alors :
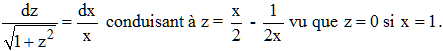
Mais z = y', d'où : y = x2/4 - ln√x + k, k constante réelle. En x = 1, y = 0 et on a finalement :
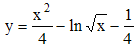
et dans ce cas le bélier ne peut rattraper l'enfant (courbe bleue) : l'axe des ordonnées est une asymptote verticale de la trajectoire du bélier car au voisinage de 0+, ln √x tend vers l'infini négatif.