ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Nombres complexes et transformations     niveau Sup        »  similitudes du plan complexe, applications affines

1°/ Montrer que l'équation ax + by + c = 0 d'une droite du plan euclidien est équivalente à son équation complexe uz + uz + v = 0 où u = a + ib et v = 2c. On pose M(x,y), M' = s(M), M'(x',y') et on note z l'affixe de M, z' l'affixe de M'.

2°/ On considère la symétrie axiale s d'axe (d) : ax + by + c = 0.

Montrer que l'expression analytique complexe de s peut s'écrire :

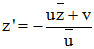
Inversement, montrer que toute transformation complexe T de la forme ci-dessus est involutive (T o T = id) et caractérise une symétrie axiale.

3°/ On considère la projection orthogonale p sur la droite (d) : ax + by + c = 0. On pose M(x,y), M' = p(M), M'(x',y') et on note z l'affixe de M, z' l'affixe de M'.

Avec les notations de 1°/, montrer que l'expression analytique complexe de p peut s'écrire :

Inversement, montrer que toute transformation complexe T de la forme ci-dessus vérifie T o T = T  et caractérise une projection orthogonale sur une droite que l'on précisera.

Ah, Ah,... Pas de solution !

C'est trop facile. Mais bon..., en cas de problème, vous pouvez me contacter...