ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Rectangle d'aire maximale pour un périmètre donné   TD niveau 3ème & LYC     »  Variante niveau 1ère , La reine Didon et les isopérimètres (niveau Sup)

De tous les rectangles qui ont le même périmètre quels sont ceux qui ont la plus grande aire ?

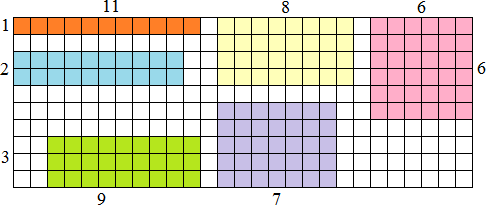
Indications :            

• Noter l la largeur du rectangle, sa longueur est L = l + k. (k ≥ 0);
• Appeler p le périmètre donné. Il s'agit de chercher la valeur de k qui maximise l'aire A du rectangle;
• Exprimer p en fonction de l et k;
• On calculera A en fonction de p et k, en éliminant l;
• Réfléchir...

Notons l la largeur du rectangle, L = l + k sa longueur (k ≥ 0) et soit p le périmètre donné. On a :

p = 4l + 2k

L'aire qu'il s'agit de maximiser est

A = l(l + k)

Exprimons l en fonction de p et k :

l = (p - 2k)/4

On reporte dans A :

Mais (p - 2k)(p + 2k) = p² - 4k². D'où :

Par conséquent, l'aire A sera maximale si le terme en soustraction est nul, donc si k = 0. C'est dire que L = l :

De tous les rectangles qui ont le même périmètre, celui qui a la plus grande aire est est le carré