Hotte tronc-pyramidale...

ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Hotte tronc-pyramidale (volume d'un tronc de pyramide) TD niveau 3ème/2nde
» Papyrus de Moscou , Hotte tronc-conique

Une hotte aspirante sera installée dans une salle de restaurant au-dessus d'un grill. Elle est constituée d'un tronc de pyramide droite de base rectangulaire.

La base inférieure a pour aire 3 m²;
la base supérieure : 0,75 m².
La hauteur de la hotte est 1,2 m.

➔ On demande de calculer le volume de la hotte afin d'estimer la puissance de la ventilation nécessaire. La difficulté de ce petit problème réside dans le fait que contrairement à l'habitude (niveau 3ème), on ne donne pas la hauteur des pyramides constituant le tronc.

Le volume d'une pyramide de hauteur h, dont l'aire de la base est B, est :

B × h/3

Le volume V cherché est la différence des volumes de la pyramide "complète" (P) et de la pyramide supérieure (p).

La pyramide (p) est une réduction de la pyramide (P) dans le rapport h'/h. Notons B' l'aire de base de (p) et H la hauteur du tronc.

Le volume cherché est :

V = (B × h - B' × h')/3

et on sait depuis la classe de 3ème que le rapport des aires est le carré du rapport des distances, donc :

B'/B = h'²/h²

Selon la formule a/b = a'/b' = (a - a')/b - b'), il suit que :

h/√B = h'/√B' = (h - h')/(√B - √B') = H/(√B - √B')

et, selon a³ - b³ = (a - b)(a² + ab + b²), le volume du tronc de pyramide d'aires de base B et B', de hauteur H est alors :

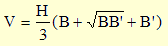
Dans notre cas, le volume du tronc de pyramide est 2,1 m³.

Une formule pour une pyramide à base carrée et une autre preuve de la formule ci-dessus : ››››