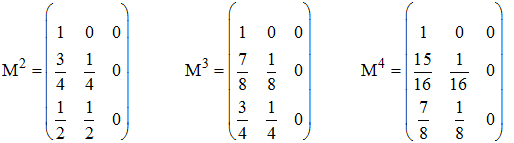Graphe et système ergodique

ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Graphe et exemple élémentaire de système ergodique niveau Sup | TD Ter ES

» Cet exemple est extrait d'un exposé manuscrit, Initiation à la théorie des graphes, de A. Kaufmann (1963) alors conseiller scientifique à la Compagnie des Machines Bull.

On suppose ici que l'hérédité d'un individu est déterminé par deux gênes A et B. Chaque individu peut présenter une association de type AA, AB -identique à BA- ou BB. Il est fréquent que l'on ne puisse pas distinguer le cas AB du cas AA : on dit que le gêne A est dominant.

Un individu est dit :

dominant (D) s'il possède l'association AA;
hybride (H) s'il possède AB (ou BA);
récessif (R) s'il possède BB.

On admet :

que les gênes transmis sont répartis aléatoirement et de façon équiprobable.
qu'un individu issu de "parents" dominants est dominant, récessif si les "parents" sont récessifs, hybride si les "parents" sont l'un dominant, l'autre récessif.

1°/ Établir le graphe probabiliste de la transmission génétique pour les trois événement possibles.

2°/ En considérant les éventualités D, H, R dans cet ordre, justifier que la matrice de transition M de ce graphe est :

3°/ Calculer M² et M³ et justifier que l'on peut conjecturer que l'expression de Mⁿ, puissance n-ème de M, est :

Justifier le bien-fondé de cette conjecture en procédant par récurrence.

4°/ Calculer la limite de Mⁿ pour n infini. En déduire que le système héréditaire (D,H,R) est ergodique, c'est à dire indépendant de son état initial, et donner l'interprétation concrète de ce résultat.

5°/ On considère le cas d'un parent dominant avec un parent de caractère inconnu. Déterminer la matrice de transition et étudier l'évolution génétique d'un tel croisement. Représenter la situation limite par un graphe.

Si vous séchez après avoir bien cherché : ››››

Solution :

1°/ On établit le graphe probabiliste du système héréditaire indiquant en étiquette la probabilité qu'un "enfant" (descendant direct) soit D, H ou R en fonction des types des parents.

Si un parent est dominant :

l'enfant reçoit A et, A ou B du second parent à chances égales. Par conséquent, l'enfant aura une chance sur deux d'être dominant ou hybride :

prob(D/D) = prob(H/D) = 1/2 et p(R/D) = 0

Si un parent est hybride :

l'enfant reçoit A ou B avec une probabilité de 1/2 et, A ou B du second dans la même proportion. Quatre éventualités, mais AB et BA sont identiques. Par conséquent, l'enfant aura 1 chance sur 4 d'être dominant, 2 chances sur 4 d'être hybride, 1 chance sur 4 d'être récessif :

prob(D/H) = prob(R/H) = 1/4 et prob(H/H) = 1/2

Si un parent est récessif :

l'enfant reçoit B et, A ou B du second parent à chances égales. Par conséquent, l'enfant aura une chance sur deux d'être récessif ou hybride :

prob(H/R) = prob(R,R) = 1/2 et p(D/R) = 0

D'où le graphe :

2°/ Pour obtenir la matrice de transition de notre système héréditaire (chaîne de Markov, car la matrice est la même pour chaque génération), l'ordre choisi étant D, H, R, on écrit en première ligne les probabilités de D, H et R sachant (que l'un des parents est) D, en seconde ligne celles de D, H et R sachant H et enfin D, H et R sachant R.

3°/ On calcule facilement :

D'où la conjecture :

s'avérant donc exacte pour n = 1, 2 et 3.

➔ Rappelons (» théorie des graphes) que P_o = (D_o, H_o, R_o), matrice ligne désignant une situation considérée comme initiale (D_o + H_o + R_o = 1) et P_n = (D_n, H_n, R_n), l'état probabiliste du système héréditaire à la n-ème génération (n ≥ 1), on aura

P_n = P_n × Mⁿ

Supposons la formule vraie pour n au moins égal à 1. On a :

En (L1,C1), vu que 8 = 2³, on a, en réduisant au même dénominateur, la fraction (2ⁿ⁺² + 2ⁿ⁺² + 8)/8 × 2ⁿ⁺², soit finalement (2ⁿ + 1)/2ⁿ⁺² : c'est le résultat espéré !
En (L1,C2), on obtient la fraction 2ⁿ/2ⁿ⁺² + 1/4, soit finalement 1/2 : c'est le résultat espéré !
En (L1,C3) : on obtient la fraction (2ⁿ⁺² + 2ⁿ⁺² - 8)/8 × 2ⁿ⁺², soit finalement (2ⁿ - 1)/2ⁿ⁺² : c'est le résultat espéré !

Les autres termes se répétant, la formule est donc confirmée par récurrence.

4°/ Lorsque n tend vers l'infini, on constate la convergence de Mⁿ vers :

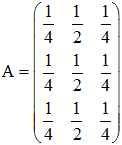
C'est dire que la limite P de P_n = (D_n, H_n, R_n) ne dépend pas de Po : à la limite, on aura en effet P = P_o × A = (1/4 1/2 1/4) puisque la somme des probabilités de P_o est D_o + H_o + R_o = 1. Le système est donc ergodique, tendant vers la situation permanente (1/4 1/2 1/4) où un "enfant" sur deux est de type hybride.

5°/ On sait ici que l'un de parents possède le caractère dominant D :

Si l'autre parent est dominant :

Il est certain que l'enfant le sera aussi :

prob(D/D) = 1, prob(H/D) = p(R/D) = 0

Si l'autre parent est hybride :

l'enfant reçoit A ou B avec une probabilité de 1/2, il ne peut pas être récessif 1 chance sur 4 d'être récessif :

prob(D/H) = prob(H/H) = 1/2 et prob(R/H) = 0

Si l'autre parent est récessif :

ce second parent est de type BB : l'enfant ne peut être ni dominant ni récessif. Donc :

prob(D/R) = 0, prob(H/R) = 1 et p(R/R) = 0

D'où le graphe :

et la matrice de transition, encore appelée M :

On calcule M² , M³ et (allez, soyons généreux) M⁴ :

On peut conjecturer :

La vérification est aisée par récurrence. On voit que Mn tend vers la matrice :

➔ Ce qui signifie que le système est ergodique, tendant vers une situation permanente (1 0 0) où les descendants posséderont de façon certaine le caractère dominant.

Le graphe montre d'ailleurs que si un descendant acquiert le caractère dominant, il le conserve : si on entre en D, on en sort plus : c'est un cas très particulier de sous-graphe transitoire.