
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
» Cet exercice est issu d'un sujet de baccalauréat français série ES, année 2003. |
 |
L'objectif est de vérifier que le graphe Γ ci-dessous est planaire par application du théorème de Kuratowski.
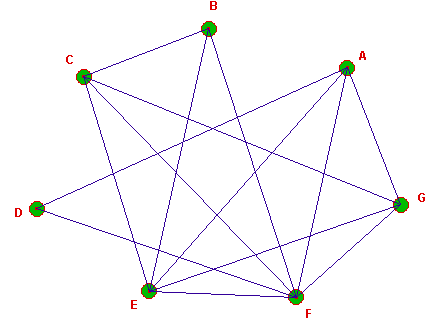
Voici la même figure générée au moyen du logiciel de géométrie dynamique Cabri Géomètre, dans sa version CabriJava pour Internet :

Si votre navigateur accepte les applets
Java
(»
extension CheerpJ![]() ) :
) :
Vous
pouvez déplacer les sommets du graphe
1°/ Justifier que ce graphe peut être contracté en supprimant D.
2°/ On obtient alors le graphe Γ ' ci-dessous :


Si votre navigateur accepte les applets
Java
(»
extension CheerpJ![]() ) :
) :
Vous
pouvez déplacer les sommets du graphe
Ecrire la matrice associée au graphe Γ ' (les sommets de Γ ' seront classés dans l’ordre alphabétique). Vérifier que Γ ' ne contient pas des graphes partiels de type I ou II (» Kuratowski).
3°/ Vérifier par déplacement des sommets que l'on peut effectivement obtenir une représentation planaire de Γ ', puis de Γ ' en rajoutant le sommet supprimé en 1°.
| Solution : |
1°/ Le sommet D n'est relié au graphe Γ que par deux arêtes aboutissant à A et F, on peut donc contracter Γ en supprimant D et remplacer DA et DF par une arête AF. Mais celle-ci existe déjà. D'où le graphe Γ ' :
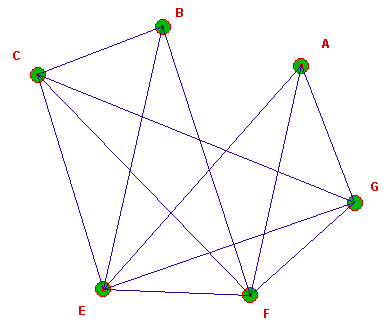

Si votre navigateur accepte les applets
Java
(»
extension CheerpJ![]() ) :
) :
Vous
pouvez déplacer les sommets du graphe
2°/
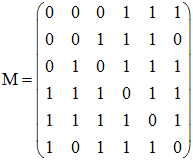
Représentation planaire de Γ ':
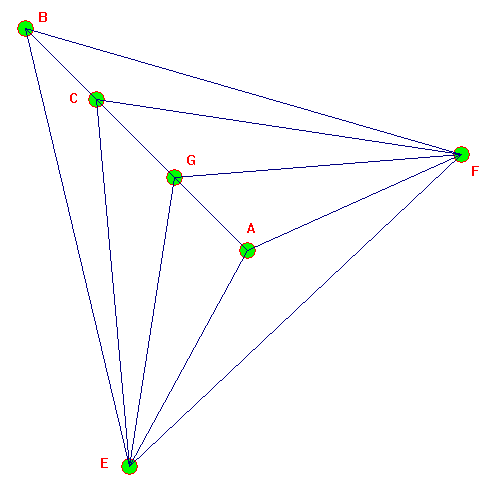
Représentation planaire de Γ ' :

Si vous le voulez et si votre navigateur le permet, vérifier maintenant par déplacement des sommets à partir du graphe d'origine :

Si votre navigateur accepte les applets
Java
(»
extension CheerpJ![]() ) :
) :
Vous
pouvez déplacer les sommets du graphe