ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Ellipse & hyperbole      niveau Ter

On considère, dans un même repère orthonormé, les courbes d'équations respectives :

(E) : x²/4 + y²/9 = 1  ,   (H)  : x²/4 - y²/9 = 1

1°/ Prouver, par une méthode ne faisant pas appel à des résultats que vous connaîtriez sur les coniques, que (E) est une courbe fermée admettant O comme centre de symétrie.

2°/ Prouver, par une méthode générale ne faisant pas appel à des résultats sur les coniques, que (H) admet deux asymptotes obliques dont on précisera les équations..

3°/ La courbe (E) est une ellipse (en bleu ciel), (H) est une hyperbole (en rouge). Ces courbes sont représentées ci-dessous :

En déduire la représentation graphique de la courbe (C) définie par : (C) : x²/4 - y| y |/9 = 1

Le changement de x en - x et de y en -y laisse l'équation inchangée : la courbe est invariante par symétrie de centre O.

On a y²/9 = 1 - x²/4, donc un point M(x,y) vérifie 1 - x²/4 ≥ 0, c'est à dire x² ≤ 4 ou encore -2 ≤ x ≤ 2. Sur cet intervalle [-2,2], on peut écrire :

Le cas y ≥ 0 correspond à une fonction f dont la représentation graphique est un arc de courbe (c), f s'annulant en x = -2 et 2.  Le cas y ≤ 0 correspond à une fonction g, opposée de f, dont la représentation graphique est un arc de courbe (c') symétrique de (c) par rapport à Ox. Les arcs (c) et (c') coïncident à leurs extrémités sur l'axe des abscisses : la courbe (E), réunion de (c) et (c') est donc fermée.

2°/ Le changement de x en -x laisse l'équation de la courbe inchangée : on peut se limiter à étudier (H) pour x ≥ 0. On a par ailleurs ici :

On peut donc se limiter à y ≥ 0. Lorsque x tend vers +∞, le rapport :

tend vers 3/2 : il y a une direction asymptotique de coefficient 3/2. Étudions maintenant y - 3x/2 :

Lorsque x tend vers +∞, y - 3x/2 tend donc vers 0. On peut donc conclure que (H) admet la droite d'équation y = 3x/2 comme asymptote oblique au voisinage de  +∞. Par symétrie par rapport à Oy et par rapport à Ox, on en déduit l'existence de deux asymptotes à (H) : y = ± 3x/2.

3°/ Deux cas peuvent avoir lieu :

• y ≥ 0 : dans ce cas, l'équation devient x²/4 - y²/9 = 1 car | y | = y. C'est dire que (c) contient la partie de (H) au-dessus de l'axe des abscisses.

• y ≤ 0 : dans ce cas, l'équation devient x²/4 + y²/9 = 1 car | y | = -y. C'est dire que (c) contient la partie de (E) au-dessous de l'axe des abscisses.

Finalement :

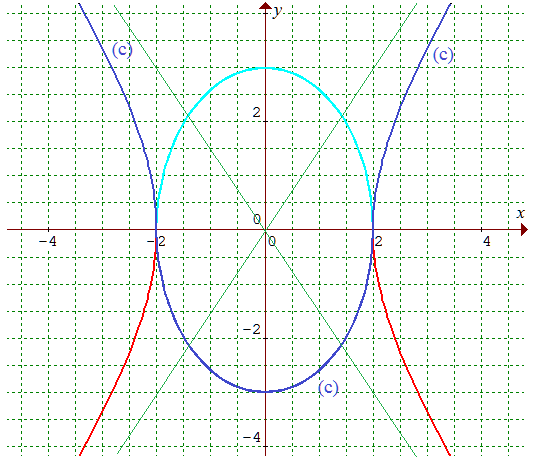
La courbe (c) est représentée en bleu foncé. Les asymptotes sont en vert fin.