
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
Né à Albi, Miquel obtient son baccalauréat de lettres puis de sciences (1834-1835) à Toulouse. Depuis 1830, Louis-Philippe est roi de France (il sera renversé par la révolution de 1848). Miquel est républicain. Il le fit savoir par des publications sociales-démocrates néfastes à sa carrière. Après une année de mathématiques spéciales à Paris, Miquel enseigne à Nantua (comme l'indique la référence Gallica) puis dans différents collèges avant de s'installer définitivement dans le Gard (collège de Bagnols/Cèze et du Vigan). Il publia de nombreux articles géométriques innovants dans le journal de Liouville.
» Un grand merci à Norbert Verdier (IUT de Cachan) pour ces informations biographiques (2005). Voir aussi réf.3 (2011).
|
Point et cercle de Miquel (1838) : |
Théorème (texte original):
Lorsque quatre points A, B, C, D sont situés sur une même circonférence de cercle ABCD; si par les points consécutifs A et B, B et C, C et D, D et A, on fait passer des circonférences de cercle, les quatre secondes intersections A', B', C', D' des circonférences consécutives se trouveront sur une même circonférence de cercle A'B'C'D'.
Autrement exprimé, on peut énoncer :
Quatre points A, B, C, D étant cocycliques, si par les points A et B, B et C, C et D, D et A, on fait passer respectivement quatre cercles, les quatre intersections de cercles A', B', C', D' ainsi produites sont cocycliques.
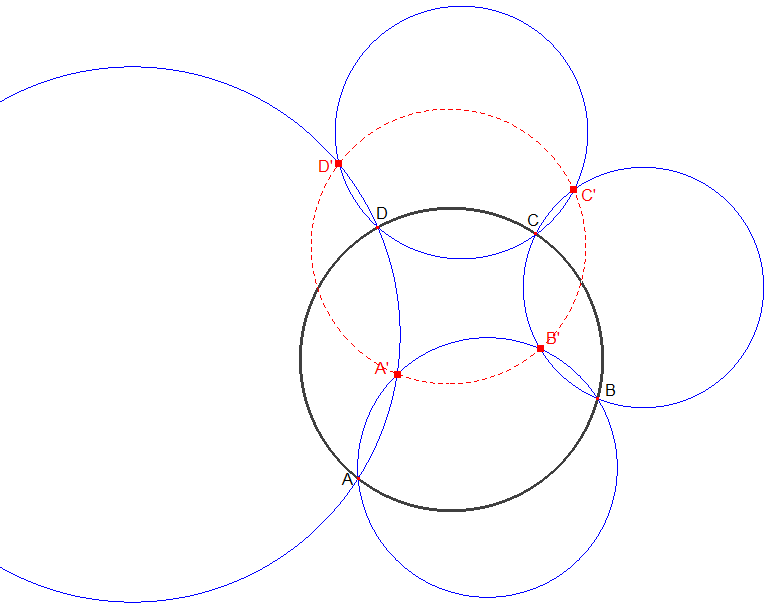
Preuve : on la trouvera sur Gallica (» réf.1), développée par Auguste Miquel dans le journal de Liouville en 1838.
Inversement, avec les mêmes notations :
Considérons trois points C, B', D' situés respectivement sur les côtés d'un triangle curviligne DBA' dont les arcs de cercle DB, BA', et A'D se coupent en un point A. Dans ces conditions, les cercles DCD', CBB' et A'D'B' sont sécants en un point C'.
∗∗∗
Point et cercle de Miquel dans le cas d'un triangle
euclidien plan :
»
➔ Pour en savoir plus :
Sur
les intersections des cercles et des sphères, A. Miquel, in journal de
Liouville (1838) :
http://gallica.bnf.fr/ark:/12148/bpt6k16382m/f525.
Géométrie,
Michèle Audin, Collection Enseignement SUP, EDP Sciences, 2006