ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 Méthode
des tangentes pour
l'équation f(x) = 0
version tableur» Version JavaScript , Autres méthodes |
Nous utilisons ici le tableur. Deux programmes sont proposées :
une approche qualifiée de descendante : itérations par recopie vers le bas;
une approche fonctionnelle : les itérations successives apparaissent dans une même cellule prévue à cet effet. C'est un processus récursif car une cellule fera appel à elle-même pour le calcul de son contenu.
Le problème est de savoir calculer une bonne approximation de f'(xo). Nous utiliserons pour ce faire l'approximation :
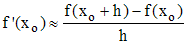
La méthode de calcul d'un nombre dérivé, dite de la dérivée symétrique, n'est pas utilisée ici car la concavité constante de la courbe assure une bonne convergence même si la tangente est en fait légèrement sécante). Notons aussi que l'on pourrait remplacer le calcul des nombres dérivés en xn par le taux d'accroissement :
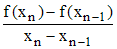
ce qui revient pratiquement à la méthode des sécantes de Lagrange, en nuisant seulement à la rapidité de convergence.
» Les calculs sont réalisés sous Microsoft Excel avec le mode d'affichage "A1", plus lisible ici que le mode "L1C1". On a choisi de résoudre l'équation sin (x) - x/2, au voisinage de xo = 2, dont la solution est sensiblement 1,89549426703.
Pour une fonction dont la définition serait plus complexe, on utiliserait une macro VisualBasic
| Approche descendante : |
En ligne 1 : xo est donné en B1 et pour le calcul de f
En ligne 2 : indications des variables nécessaires à notre programme : en particulier, en colonne F, dxn = | xn+1 - xn| permet d'apprécier la convergence.
En ligne 3 : le compteur d'itération n est mis à 0. Au départ, xn= xo. En C3, on définit f(x), B3 représentant la variable x. D'après la formule de récurrence de la version JavaScript, dxn n'est autre que la valeur absolue de f(xn)/f
En ligne 4 : le compteur n est incrémenté par : =A3 + 1 et on recopie vers le bas (symbole
| A | B | C | D | E | F | |
| 1 | Xo= | 2 | h= | 0,001 | ||
| 2 | n | Xn | f(Xn) | f(Xn+h) | f'(Xn) | dXn |
| 3 | 0 | =B1 | =SIN(B3)-B3/2 | =SIN(B3+h)-(B3+h)/2 | =(D3-C3)/h | =ABS(C3/E3) |
| 4 | =A3+1 | =B4-C4/E4 | ↓ | ↓ | ↓ | ↓ |
| 5 |
↓ |
↓ |
| Compte rendu d'exécution : |
| Xo = | 2 | h= | 0,001 | ||
| n | Xn | f(Xn) | f(Xn+h) | f'(Xn) | dXn |
| 0 | 2 | -0,091 | -0,091619 | -0,917 | 0,09895531 |
| 1 | 1,901044694 | -0,005 | -0,005385 | -0,825 | 0,00552957 |
| 2 | 1,895515128 | -2E-05 | -0,000837 | -0,82 | 2,0849E-05 |
| 3 | 1,895494279 | -1E-08 | -0,00082 | -0,819 | 1,2306E-08 |
| 4 | 1,895494267 | -6E-12 | -0,000819 | -0,819 | 7,1153E-12 |
| 5 | 1,895494267 | -3E-15 | -0,000819 | -0,819 | 3,9288E-15 |
On constate la convergence extrêmement rapide du procédé (5 itérations donnent un résultat plus que convenable...).
➔ On pourra étudier l'effet d'un changement des valeurs initiales de xo ou h. Ces deux valeurs sont liées ! Lorsque la courbe ne change pas de concavité dans l'intervalle ]x - h, x + h[ et si, dans cet intervalle, il n'y a pas une autre solution de l'équation f(x) = 0, la convergence est assurée. ! Mais attention : un h "trop petit" peut conduire à des résultats aberrants : dérivée nulle en particulier car l'ordinateur risque alors de ne plus distinguer entre f(x + h) et f(x) : si h << 1 alors, pour la machine, x + h = x.
| Approche fonctionnelle (récursion) : |
Nous donnons un nom à chaque cellule (à droite de l'égalité mathématique) afin de mieux appréhender le programme. Remarquer alors l'absence de références à des cellules du type =B3-C3/E3 : l'écriture de l'algorithme est plus mathématique.
En gras, et à gauche de leur définition, sont les variables nécessaires au programme. Les noms attribués à ces définitions sont :
Xo pour xo , h pour h , Yn pour f(xn) , Ynh pour f(xn + h)
Ypn pour f'(xn) , d pour d (drapeau) , n pour n (compteur) , Xn pour xn (référence circulaire)
On se place en mode itération en fixant le
nombre d'itérations à 1 : on relancera le calcul
à chaque fois (
= sur
Apple, Ctrl = sur
PC), ce qui permet de lire les résultats intermédiaires
et d'apprécier la convergence.
Les approximations successives apparaissent
à droite de la cellule , raison pour laquelle la
méthode est dite fonctionnelle. Si le drapeau d est mis
à 0, le programme est initialisé. Si d est mis à
1 par l'utilisateur le programme commence à itérer. La
convergence est très rapide, l'affichage de Xn reste constant
dès la 6e itération.
i Si
on applique la méthode de Newton à la fonction
√x, de fonction dérivée x →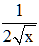
, les formules de récurrence de Newton et de Héron
d'Alexandrie coïncident.
| A | B | C | D | |
| 1 | Xo= | 2 | d= | 1 |
| 2 | h= | 0,001 | ||
| 3 | n= | =SI(d=0;0;n+1) | Xn= | =SI(d=0;Xo;Xn-Yn/Ypn) |
| 4 | f(Xn)= | =SIN(Xn)-Xn/2 | dXn= | =ABS(Yn/Ypn) |
| 5 | f(Xn+h)= | =SIN(Xn+h)-(Xn+h)/2 | ||
| 6 | f'(Xn)= | =(Ynh-Yn)/h |
| Compte rendu d'exécution : |
| A | B | C | D | |
| 1 | Xo= | 2 | d= | 1 |
| 2 | h= | 0,001 | ||
| 3 | n= | 100 | Xn= | 1,89549426703398 |
| 4 | f(Xn)= | 0 | dXn= | 0 |
| 5 | f(Xn+h)= | -0,0008195 | ||
| 6 | f '(Xn)= | -0,8194963 |
Autres méthodes : »