
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
➔ Texte original. Seuls sont modifiés la mise en page, quelques tournures et aspects orthographiques ou grammaticaux Les mots ou les commentaires en vert sont ajoutés pour une meilleure compréhension.
FONCTION, s. f. (Algèbre) les anciens géomètres, ou plutôt les anciens analystes ont appelé fonctions d'une quantité quelconque x les différentes puissances de cette quantité (voyez PUISSANCE) ; mais aujourd'hui on appelle fonction de x, ou en général d'une quantité quelconque, une quantité algébrique composée de tant de termes qu'on voudra & (et) dans laquelle x se trouve d'une manière quelconque, mêlée, ou non, avec des constantes. Ainsi,

sont des fonctions de x.
 » Remarquer que d'Alembert utilise
indifféremment x2 et xx pour exprimer un carré. Noter aussi
que sa définition
se limite aux seules fonctions algébriques. La fonction exponentielle y
= ax, par exemple, est étudiée en tant que courbe dans
le cadre de la géométrie transcendante.
On pourra consulter l'ensemble de l'encyclopédie en suivant les deux
liens présents en fin de page.
» Remarquer que d'Alembert utilise
indifféremment x2 et xx pour exprimer un carré. Noter aussi
que sa définition
se limite aux seules fonctions algébriques. La fonction exponentielle y
= ax, par exemple, est étudiée en tant que courbe dans
le cadre de la géométrie transcendante.
On pourra consulter l'ensemble de l'encyclopédie en suivant les deux
liens présents en fin de page.
De même x2y + ay3, &c (etc.). est une fonction de x & de y, & ainsi des autres.
Tous les termes d'une fonction de x sont censés avoir la même dimension; quand ils ne l'ont pas, c'est qu'il y a une constante sous entendue qu'on prend pour l'unité, ainsi dans x2 + y3, on doit regarder x2 comme égale à ax2, a étant l'unité.
Quand la fonction n'est ni fraction ni radical, sa dimension est égale à celle d'un de ses termes. Ainsi la fonction x2 + x3 est de trois dimensions.
Quand la fonction est une fraction, la dimension est égale à celle du numérateur moins celle du dénominateur. Ainsi,
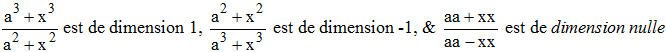
Voyez TAUTOCHRONE & INTEGRAL.
Quand la fonction est radicale, sa dimension est égale à celle de la quantité qui est sous le signe, divisée par l'exposant du radical ;
Ainsi
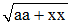 est de 2/2 = 1 dimension
est de 2/2 = 1 dimension
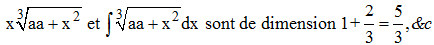 & ainsi des autres.
& ainsi des autres.
Fonction homogène est une fonction de deux ou plusieurs variables x, y, &c. dans laquelle la somme des dimensions de x, y, &c. est la même. Ainsi x2y + ax3 + by3 est une fonction homogène ; il en est de même de :

Voyez HOMOGENE & INTEGRAL.
Fonctions semblables sont celles dans lesquelles les variables & les constantes entrent de la même manière ; ainsi a a + x x & A A + X X sont des fonctions semblables des constantes A, a, & des variables X, x.
Jean le Rond d'Alembert
Nombre négatif selon d'Alembert : » Règle des signes selon d'Alembert : »
➔ Pour en lire ou savoir plus :
L'encyclopédie :
- Sur Lexilogos (en fait, ARTFL, Encyclopedice
Project de l'université de Chicago) :
http://www.lexilogos.com/encyclopedie_diderot_alembert.htm
Dans les textes non numérisés, les formules
mathématiques
sont absentes, mais le site propose généralement un lienvers la page d'origine).
- Sur le site Gallica de la B.N.F :
http://gallica.bnf.fr
(Dictionnaires ==> Encyclopédies & Dictionnaires généraux).