ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Divergence spirale d'une suite récurrente        » Étudier tout d'abord le cas plus simple de la  convergence "spirale"

On se propose d'étudier la suite récurrente (u_n) définie par :

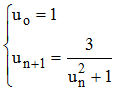
afin de montrer qu'un calcul naïf de sa "limite" conduit à une erreur mathématique...

1°/  Si la suite possède une limite L, elle vérifie L = 3/(L² + 1) c'est à dire :

L³ + L - 3 = 0

Montrer que la fonction h : x → x³ + x - 3 est strictement croissante et s'annule au voisinage de α = 1,213. 

2°/  Cette valeur positive, acceptable a priori pour L, ne correspond à aucune observation plausible eu égard au graphique fourni par le tableur.

Le mode courbe visualise (ci-dessous) les variations de la suite en reliant les points (n,u_n). Le graphique montre une "anomalie" :

 ➔   les valeurs prises par la suite semblent s'accumuler alternativement au voisinage de 2,618... et de 0,38196... Cette alternance nous conduit à penser que les suites extraites v_n = u_2n et w_n = u_2n+1 sont convergentes, l'une décroissante, l'autre croissante.

On pose :

Tracer la courbe x → f(x) sur l'intervalle [0;3] dans un repère orthonormé d'unité 4 cm. Tracer la droite (d) d'équation y = x.

On a :

• u₁ = f(u_o) = 1,5; on reporte cette valeur sur (d); on en déduit :

• u₂ = f(u₁); on reporte cette valeur sur (d); on en déduit :

• u₃ = f(u₂); on reporte cette valeur sur (d); on en déduit :

• ...

• u_n+1 = f(u_n);

• ...

Programme JavaScript de contrôle de convergence d'une suite  u_n = f(u_n-1):  »

 ➔   La valeur a = 1,213... se retrouve ci-dessus comme abscisse de l'intersection de C_f et de (d). On constate une divergence en spirale avec une accumulation des valeurs au voisinage de 2,6 et 0,4.

Étudions ce phénomène :

3°/  Étudier les variations de f sur l'intervalle J = [0;3]; en déduire les résultats suivants :

• f(J) ⊂ J;

• 0 < u_n < 3 pour tout n de N;

• f est strictement décroissante;

• f o f est strictement croissante.

4°/  Vérifier que l'on a  u₃ > u₁ mais u₂ < u₀ et utilisant que f o f est strictement croissante, prouver que les suites extraites (v_n) et (w_n) définies pour tout n par v_n = u_2n et w_n = u_2n+1 sont respectivement strictement décroissante et strictement croissante.

5°/  Déduire des résultats précédents la convergence des deux suites (v_n) et (w_n).

6°/  On note respectivement v et w les limites des suites (v_n) et (w_n). Justifier que ces limites sont distinctes et solutions du système :

Montrer alors que v et w sont les solutions de l'équation x² - 3x + 1 = 0. 

On a :

 ➔   Les valeurs v et w sont des points d'accumulation de la suite (u_n).