
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
Cet algorithme de recherche du chemin optimal sur un graphe est équivalent à celui de Ford-Fulkerson. Outre le livre de Berge/Ghouila-Houri (programmes, jeux et réseaux de transports, 1962, » réf.1) qui reste encore aujourd'hui une excellente référence, on trouvera (» réf.2, site Interstices) un lien explicitant, en particulier, les algorithmes de Bellman-Kalaba et de Roy-Warshall-Floyd.
On suppose ici connu le vocabulaire élémentaire de la théorie des graphes. On considère un graphe pondéré orienté ou non. On cherche à optimiser un chemin d'origine E (appelée entrée), d'extrémité S (sortie).
Par optimiser, on entend par exemple, suivant les cas, minimiser une distance de E à S, un coût de transport, un flux énergétique, une durée (itinéraire GPS), etc. Lorsque le graphe est orienté, il s'agira bien entendu de suivre les sens autorisés indiqués. Les poids (étiquettes) du graphe doivent être positives. L'algorithme de Bellman-Kalaba autorise des étiquettes de signes contraires.
! Dans un graphe orienté, un chemin ou un circuit peut rendre le problème insoluble ! à gauche ci-dessus, depuis E ou D, il est manifestement impossible de se rendre en F ou C. Mais depuis A, F ou C, on peut parcourir entièrement le graphe :

Exemple 1 (bac ES) :
Étudions l'algorithme de Dijkstra sur cet exemple (sujet bac ES, Centres étrangers, juin 2003, » sujet complet et corrigé en réf.6) : le graphe ci-dessous est orienté :
Il s'agit de se rendre de C à A en minimisant les temps de parcours indiqués
On trouve ici une unique solution :
Afin de ne pas s'embrouiller dans le déroulement de l'algorithme, il est fortement conseillé, voire obligatoire, d'utiliser un tableau dont les en-têtes des colonnes seront les sommet. La dernière colonne (sommets "fixés") indique les sommets successivement jugés être optimums.
! On verra que cette optimalité peut changer au cours de l'algorithme.
Initialisation de l'algorithme :
➔ L'ordre des sommets dans le tableau est tout à fait arbitraire. Il est cependant naturel de les écrire de gauche à droite semblablement à la lecture du graphe (se rendre de C à A en minimisant les temps de parcours) :
| C | B | F | D | E | A | Fixés |
| 0 | 9C | 6C | 2C | ∞ | ∞ | C |
Cheminement :
Tant que le point de sortie n'a pas été atteint, c'est à dire non fixé, on itère ligne par ligne de la façon suivante :
i/ On repère le poids P le plus faible
: c'est ici 2C correspondant au sommet D.
On fixe D en retenant 2C (signalé ci-dessous en
jaune) et on ferme sa colonne (grisée
ci-dessous).
2i/ On inscrit en ligne suivante les distances de ce point aux autres sommets adjacents du graphe à l'exception des points déjà fixés (colonnes orange) augmentées du poids P.
3i/ Si en faisant cette somme on trouve, pour un sommet, un poids inférieur au poids inscrit précédemment, on inscrit ce nouveau poids suivi de sa provenance.
4i/ Si le poids est identique ou supérieur
(∞ en particulier), on conserve l'ancien et sa provenance.
»
lorsque le poids est identique, le remplacer par
la nouvelle provenance peut introduire un sommet supplémentaire dans le
chemin final
(voir le second exemple).
| C | B | F | D | E | A | Fixés |
| 0 | 9C | 6C | 2C | ∞ | ∞ | C |
| D | ||||||

Poursuite de l'algorithme :
Depuis D : B n'est pas adjacent, on reconduit 9C (et non pas ∞ selon 4i/). De D à F, on à 3 auquel s'ajoute 2, on inscrit donc 5D. De D à E, pas possible, on conserve ∞ pour ce point. De D à A, on a 9 auquel s'ajoute 2, soit 11 < ∞; on inscrit donc 11D. Finalement, passer par F s'avère minimal : on fixe F et on ferme sa colonne en retenant 5D :
| C | B | F | D | E | A | Fixés |
| 0 | 9C | 6C | 2C | ∞ | ∞ | C |
| 9C | 5D | ∞ | 11D | D | ||
| F | ||||||
Depuis F : de F à B, le graphe indique 3 auquel s'ajoute 5, soit 8F (selon 3i/). De de F à A, on a 6 auquel s'ajoute 5, soit 11 : on maintient donc 11D (selon 4i/). à cette étape, on fixe B, on ferme sa colonne et on retient 8F :
| C | B | F | D | E | A | Fixés |
| 0 | 9C | 6C | 2C | ∞ | ∞ | C |
| 9C | 5D | ∞ | 11D | D | ||
| 8F | ∞ | 11D | F | |||
| B | ||||||
Depuis B : on obtient 10 en A : on inscrit 10B meilleur que 11D. De B à E n'est toujours pas adjacent, donc ∞ pour E et l'algorithme se termine. On peut fixer A pour le principe, d'où l'inscription finale 0 :
| C | B | F | D | E | A | Fixés |
| 0 | 9C | 6C | 2C | ∞ | ∞ | C |
| 9C | 5D | ∞ | 11D | D | ||
| 8F | ∞ | 11D | F | |||
| ∞ | 10B | B | ||||
| 0 | A |

Chemin optimal :
On remonte en arrière les sommets fixés (colonne orange) :
A, point de sortie, provient de B
B provient de F
F provient de D
D provient de C : point d'entrée.
D'où le chemin C D F B A de poids 10.
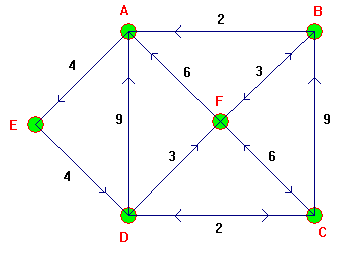
Exemple 2 :
Voici un exemple de graphe non orienté dont la solution n'est pas unique. Il s'agira de trouver la distance minimale tout en minimisant également le nombre de sommets obtenus, ce qui concrètement éviterait les encombrements d'une ville supplémentaire à traverser :

| E | A | B | C | D | F | S | Fixés |
| 0 | 4E | 2E | ∞ | ∞ | ∞ | ∞ | E |
| 4E | 7B | ∞ | 5B | ∞ | B | ||
| (7A) 7B | 9A | 5B | ∞ | A | |||
| 7B | 9A | 13F | F | ||||
| 8C | 12C | C | |||||
| (12D) 12C | D | ||||||
| 0 | S |
Chemin optimal :
On remonte en arrière les sommets fixés :
S, point de sortie, provient de C
C provient de B
B provient de E : point d'entrée.
D'où le chemin E B C S de poids 12.
Cette solution n'est pas unique : en C, on aurait pu choisir A plutôt que B : on a 7A et 7B, d'où une seconde solution de même poids 12 : E A C S.
En S, on aurait pu introduire D au lieu de conserver C. Mais D provient justement de C, d'où deux chemins supplémentaires à 3 sommets intermédiaires de poids 12 :
E B C D S et E A C D S
Comme nous voulions minimiser le nombre de sommets, on conclut qu'il y a deux solutions équivalentes de poids 12 :
E A C S et E B C S
∗∗∗
Autres exemple sur le site PanaMaths : graphe eulérien et
plus court chemin (Bac ES 2004) : réf.7
➔ Pour en savoir plus :
Programmes, jeux et réseaux de transport, par Claude Berge et A. Ghouila-Houri, Ed. Dunod Paris - 1962.