ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
» La version JavaScript et une accélération de convergence vous seront exposées en cliquant sur la clé. |
Dans son Logarithmotechnia, Mercator calcule l'aire sous l'hyperbole x → 1/x, en exhibant le développement :
x - x2/2 + x3/3 - x4/4 + x5/5 - ... (série de Mercator)
correspondant au développement en série de la fonction x → ln(1 + x) pour | x | ≤ 1.
Lorsque x = 1, la série est alors appelée série harmonique alternée, sa somme est ln 2 :
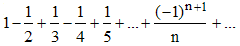
Selon un résultat de Leibniz, cette série étant alternée, l'erreur faite en limitant la somme au rang n est inférieure au terme de rang n + 1, donc inférieure à 1/n : la convergence sera donc certainement très lente.
| Programme sur tableur : |
colonne A : rang n. La colonne est baptisée n : Insertion... Nom... Définir
colonne B : on pourrait utiliser la fonction puissance du tableur : (-1)^n mais pour une alternance de signe suivant la parité de n, il est plus "joli" d'écrire :
➔ la fonction MOD(a,b) retourne le reste de la division de a par b.
colonne C : il n'y a plus qu'à faire la somme des termes en initialisant C2 à B2; C3 contiendra C2 + B3 et on recopiera les formules vers le bas autant que désiré.

| Résultat d'exécution. Rappel : ln 2 = 0,6931471805599... : |

| et vers n = 1000, on approche de la valeur approchée à 1/1000 près... : |