
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
TD niveau 5è/3è » en 3ème, on pourra utiliser la propriété de Thalès "croisée" |
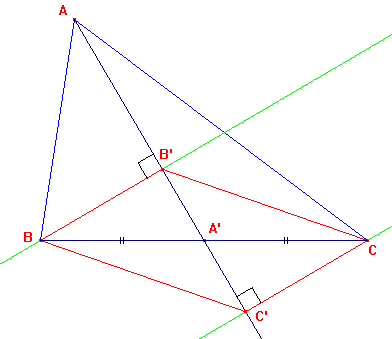
Observe la figure ci-dessus :
On a tracé un triangle ABC et la médiane issue de A. Le point A' est le milieu de [BC];
On a tracé les perpendiculaires à (AA') issues de B et de C; elles coupent (AA') en B' et C';
On a tracé [BC'] et [B'C].
Il semble que BB'CC' soit un parallélogramme. Prouve-le en utilisant la symétrie de centre A'
➔ Élève de 3ème ? allergique aux symétries ? Tu peux utiliser la propriété de Thalès dans sa configuration dite "croisée" ou "papillon"...
Indications :
Puisque A' est le milieu de [BC], dans la symétrie s de centre A', le symétrique de B est le point C.
Justifie que les droites (BB') et (CC') sont parallèles.
Justifie que la droite (AA') est invariante dans la symétrie s.
Prouve maintenant que l'image par s de (BB') est (CC')

Complète :
Le point B' est situé sur (.....) et sur (.....), par conséquent son symétrique est à la fois sur (.....) et sur (.....) : c'est donc le point C'.
Conclusion :
Les diagonales du quadrilatère BB'CC' ont donc le même milieu A' : c'est un parallélogramme.
➔ En 3ème, on peut utiliser la propriété de Thalès et rédiger ainsi :
Les droites (BB') et (CC') sont parallèles car toutes deux perpendiculaires à (AA').
Les droites (BC) et (B'C') sont sécantes en A', les droites (BB') et (CC') sont parallèles : en vertu de la propriété de Thalès (configuration croisée), on a A'B'/A'C' = A'B/A'C.
Or A'B/A'C = 1/2 puisque A' est le milieu de [BC], donc A'B'/A'C' = 1/2; c'est dire que A' est aussi le milieu de [B'C']. Et la conclusion est la même que la précédente.