
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

 |
|
On considère un triangle ABC. On note M le milieu de [AC].
On suppose que DB est le tiers de CB. Le
segment [BM] coupe [AD] en F.

Montrer que FD est le quart de AD
Indications, solution à compléter :
Tracer [ME] où E est le milieu de [CD], des parallèles semblent apparaître... Observe maintenant bien la figure obtenue et complète la solution proposée :
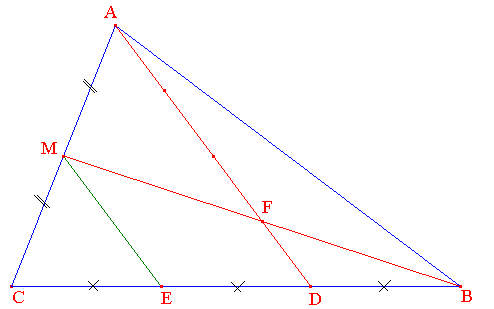
M est le ............... [AC], E est le ............... de [CD].
Si un segment joint les
............... de deux côtés d'un
triangle, sa ................ est la ............... de celle du
............... côté.
De cette propriété, je déduis que dans le triangle ACD, on a AD = .........
Comme D est au 1/3 de CB à partir de B, D
est au ........ de CB à partir de C et comme E est le milieu de [CD], je
déduis que
CE =
....... = DB et que D est donc le ............ de [EB].
Dans le triangle MBE, on peut affirmer selon la propriété 2 que ME = 2 FD et comme AD = 2ME, nous avons : AD = 4FD.
C'est dire que FD est le quart de AD, ce qu'il fallait démontrer.