ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Un problème massif  #2     équation se ramenant au 1er degré      niveau 4ème             variante rectangulaire (second degré)

• Un massif fleuri de forme circulaire est entouré d'une allée de 1,50 m de large.

• Afin de prévoir la quantité de désherbant à utiliser dans l'allée, le jardinier a évalué précisément l'aire de celle-ci : il a trouvé 165 m².

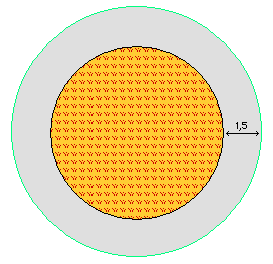
     Quelles est le rayon du massif  ?
     (on arrondira au mètre le plus proche)

• On procède par différence des aires : si r est le rayon cherché, on a :

p(r + 1,5)² - pr² = 165

L'équation se réduit à 3pr + 2,25p = 165, soit (en prenant 3,14 comme valeur approchée de p) : r = 157,935 / 9,42 = 16,7659...

Au moyen de la touche p de la calculatrice : 165 - 2.25 x p  EXE  ÷ 3  ÷ p  EXE, on obtiendra r = 16.7570...

  Diviser par 3p, c'est diviser par 3 puis diviser par p !

• Réponse : selon la consigne de l'énoncé , on pourra donc répondre r = 17 m.