ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Approche fonctionnelle de sinh et cosh

On se propose ici de "construire" les fonctions sinus et cosinus hyperboliques à partir de leurs propriétés fondamentales de la façon suivantes :

1. f et g sont deux fonctions numériques au moins deux fois dérivable sur R.
2. Pour tout réel x, f ²(x) - g²(x) = 1
3. Pour tous réels x et y :
      •  a/  f(x + y) = f(x)f(y) + g(x)g(y)
      •  b/  g(x + y) = g(x)f(y) + f(x)g(y)

On appellera P1, P2, P3a et P3b ces propriétés.

1°/ En utilisant P2, justifier que f ne s'annule pas sur R et au moyen de P2 et P3a, montrer que f(0) = 1, puis g(0) = 0.

2°/ Pour tout x réel, on pose u = f(-x) et v = g(-x). Écrire P3a et P3b lorsque y = -x et exprimer u et v en fonction de f(x) et g(x). Quelle conclusion peut-on tirer de ces résultats ?

3°/ Calculer  f'(0) puis f"(0).

4°/ En utilisant P3a, calculer f'(x) en fonction de g(x) et g'(0). Calculer ensuite g'(x) et exprimer f"(x) en fonction de f(x).

5°/ Soit ω un réel non nul. Résoudre l'équation différentielle y'' = ω²y.

6°/ Montrer que f(x) = ch(ωx) est la solution du problème. Que dire alors de g ?

1°/  On a f ²(x)  = 1 + g²(x) ≥ 1 : f ² ne peut donc pas s'annuler et par conséquent, il en est de même pour f.

P3a fournit, avec x = y = 0 :  f(0) = f ²(0) + g²(0) et P2 indique que g²(0) = f ²(x) - 1. En posant X = f(0), on obtient l'équation 2X² - X - 1 = 0. Donc X = 1 ou X = -1/2. Cette dernière possibilité est à rejeter puisque f(0), somme de deux carrés, est positif ou nul. D'où f(0) = 1, dont on déduit g(0) = 0.

2°/ On obtient f(x) × u + g(x) × v = 1 et g(x) × u + f(x) × v = 0. C'est un système d'équations linéaires. Son déterminant est f ²(x) - g²(x) = 1 ≠ 0. On en déduit l'unique solution u = f(x) et v = g(x). Par conséquent, f est paire et g est impaire.

3°/ f étant paire, on a pour tout x réel : f(x) = f(-x), donc f'(x) = [f(-x)]' = - f'(-x). En x = 0, on a f'(0) = - f'(0), donc f'(0) = 0.  » Résultat connu : si f est paire (resp. impaire), sa dérivée est impaire (resp. paire).

 Dérivons deux fois la relation f ²(x) - g²(x) = 1. On obtient :

f'²(x) + f(x)f"(x)  - g(x)g''(x) - g'²(x) = 0. Faisons x = 0, il vient : f"(0) = [g'(0)]².

4°/ Calculons f(x + y) - f(x). D'après P3a, il vient f(x + y) - f(x) = f(x)f(h) + g(x)g(h) - f(x). D'où :

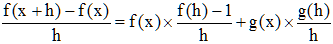
De f(0) = 1 et g(0) = 0, on déduit que lorsque h tend vers 0, f'(x)  = f(x) f'(0) + g(x)g'(0), soit f'(x)  = g(x)g'(0) puisque f'(0) = 0.

Un calcul strictement semblable conduit à g'(x) = f(x)g'(0). Par suite :

f"(x) = g'(x) g'(0) = f(x)[g'(0)]² = f"(0)f(x)

5°/  L'équation caractéristique est r² - ω² = 0, donc r = ± ω. C'est dire que la solution générale est de la forme  y = αe^ωx + βe^-ωx.

6°/ Puisque f"(0) = [g'(0)]², on peut écrire f"(x) = ω²f(x).

Dire que ω est nul, c'est dire que f"(0) = 0, donc que f"(x) = 0 pour tout x de R. f est alors de la forme ax + b. La fonction f étant paire, on a nécessairement a = 0 et vu que f(0) = 1, il vient b = 1. Donc f(x) = 1 pour tout x et de P2, on tire g(x) = 0 pour tout x.

Si ω est non nul, on peut écrire f(x) = αe^ωx + βe^-ωx. La fonction f étant paire : f(x) = f(-x) entraîne (α - β)(e^ωx - e^-ωx) = 2(α - β)sh(ωx). ω étant non nul, ceci n'est possible que si α = β et on obtient la fonction f(x) = α(e^ωx + e^-ωx) avec la condition f(0) = 1, donc α = 1/2. D'où f(x) = ch(ωx).

Que dire de g ?  

On a g²(x) = ch²(ωx)  - 1 =  sh ²(ωx), donc g(x) = ± sh(ωx). On vérifie immédiatement que les hypothèses P1, P2 et P3 sont vérifiées par :

• ∀ x∈R, f(x) = ch(ωx), g(x) = sh(ωx)

ou bien :

• ∀ x∈R, f(x) = ch(ωx), g(x) = -sh(ωx)

 ➔  g étant non identiquement nulle, le cas mixte où g(x) = sh(ωx) pour certaines valeurs isolées ou non de x et g(x) = -sh(ωx) pour d'autres ne peut avoir lieu par continuité de g (et invaliderait d'ailleurs P3a).

En conclusion, f et g sont respectivement x → ch(ωx) et x → sh(ωx) ou bien x → ch(ωx) et x → -sh(ωx), et on remarque que le cas f(x) = 1, g(x) = 0 pour tout x de R correspond à ω = 0.