ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 
Fonction de répartition
(cas continu),
densité niveau Supespérance mathématique, variance |
Soit X la variable aléatoire continue dont la fonction de répartition est définie par :
où λ désigne un nombre réel convenable.
1°/ a - Quelle est la densité de X ? Que
doit être la valeur de λ ?
b - Représenter en justifiant brièvement les
courbes représentatives de F et f.
2°/ Calculer l'espérance mathématique E(X) de X.
3°/ X admet-elle une variance V(X) ?
| Solution : |
1°/ a- La densité f de X est la fonction dérivée de sa fonction de répartition F. Par conséquent :
La condition sur λ est :
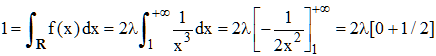
Donc λ = 1.
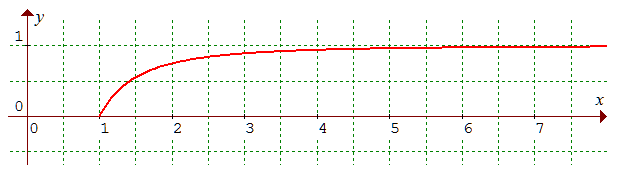
b - Représentation graphique de la fonction de répartition F de X :
F(x) = 1 - 1/x2 sur [1,+∞[. C'est une fonction strictement croissante (de dérivée f), nulle en 1 et admettant y = 1 comme asymptote horizontale à l'infini.
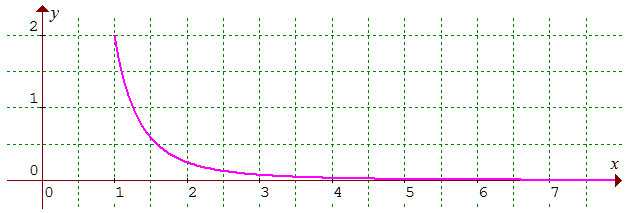
Représentation graphique de la densité f de X :
f(x) = 2/x3 sur [1,+∞[. C'est une fonction strictement décroissante, égale à 2 en x = 1 et admettant (Ox comme asymptote horizontale à l'infini.
2°/ L'espérance mathématique de X est donnée par :
3°/ La variance de X est donnée par :
Mais cette intégrale diverge car la limite de ln à l'infini est infinie. X n'admet pas de variance.
Interprétation :
Selon le calcul précédent, l'écart-type de X, racine carrée de sa variance et mesurant la dispersion moyenne des valeurs de X autour de sa moyenne, est donc infini. Cela s'explique par le "déséquilibre" de la distribution de probabilités comme le montre la courbe représentative de F : la moyenne des valeurs de X est E(X) = 2.
On a Prob(X < 2) = F(2) = 1 - 1/4 = 0,75. Donc Prob(X > 2) = 0,25 : probabilité non négligeable. Noter que si la densité "s'étalait" sur R tout entier, le terme à intégrer dans V(X), à savoir 1/x, fonction impaire, assurerait une variance nulle.