ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Étude d'une fonction numérique      niveau Sup    (BTS informatique industrielle)        usage d'un développement limité d'ordre 3

On considère la fonction f définie pour tout réel x par :

où ln désigne la fonction logarithme népérien.

1°) Montrer que f vérifie l'équation différentielle du 1er ordre :

2°) Calculer f(0), puis utiliser 1° afin de calculer f'(0), f''(0) et f'''(0). En déduire le développement limité d'ordre 3 de f au voisinage de 0.

3°) En remarquant que 1 = 1 + e^t - e^t, calculer l'intégrale (x désigne un nombre réel) :

En déduire, en utilisant 1°, l'expression de la primitive de F, nulle en 0, à savoir :

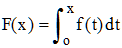
4°) Justifier l'écriture ln(1 + e^-x) = ln(1 + e^x) - x. Calculer la limite de F pour x infini positif ainsi que celle de F(x) - x pour x infini négatif.

5°) Justifier brièvement que f est strictement croissante et donner l'allure de sa courbe représentative dans un repère orthonormé.

1°) On a f(0) = ln2. En dérivant la fonction f, On obtient sans difficultés f'(x) = 1/(1 + e^x) - f(x). D'où le résultat annoncé :

dont on déduit f'(0) = ½ - ln2.

2°) En dérivant la formule ci-dessus, on obtient y' + y'' = -e^x/(1 + e^x)². D'où f''(0) = ln2 - ¾. En dérivant encore une fois :

On remplace x par 0 pour obtenir : f'''(0) =  ¾ - ln2. On peut donc écrire au voisinage de 0 :

3°) Vu l'indication donnée, on peut écrire :

Selon 1°, on peut écrire f(x) = 1/(1 + e^x) -  f'(x). Donc :

Ce qui peut s'écrire :

4°) On peut écrire successivement :

ou bien, plus rapidement :

On peut donc écrire :

Lorsque x tend vers +∞, e^-x tend vers 0, donc ln(1 + e^-x) tend vers ln1 = 0. 
D'autre part, X = e^x tend vers +∞,donc ln(1 + X)/X ≈ ln(X)/X tend vers 0. Par conséquent, F a pour limite 2ln2 en +∞.

Selon 3°, on a :

Lorsque x tend vers -∞, X = e^x tend vers 0, donc ln(1 + e^x) tend vers ln1 = 0.  D'autre part ln(1 + X)/X tend vers 1.
Par conséquent, F(x) - x a pour limite 2ln2 - 1 en +∞.

5°) Vu que e^x est strictement positive, on a 1 + e^x > 0, donc f(x) > 0 pour tout x. On en déduit que F est strictement croissante. Sa courbe représentative passe par l'origine et admet, selon 4°, deux asymptotes d'équations respectives y = 2ln2 et y = x + 2ln2 - 1 :